W moich wcześniejszych wpisach pojawiały się wskaźniki, opisujące wyniki inwestycji czy rezultaty testów systemów automatycznych i okazuje się, że nie dla wszystkich są one zrozumiałe. Zostałem poproszony o rozwinięcie skrótów pod którymi owe miary się kryją i krótką charakterystykę każdej z nich. To była jedna prośba z tych, których się nie odmawia. Mam nadzieje, że w ten sposób przyszłe wpisy będą dużo czytelniejsze.
Wynikiem symulacji na danych w dowolnym programie używanym do tworzenia systemów transakcyjnych jest standardowy raport, w którym otrzymujemy dość pokaźną statystykę, opisującą zmiany kapitału w trakcie testu. Ale oczywiście te same mierniki możemy uzyskać podczas ręcznego przeliczenia wyników dowolnej inwestycji czy też przy użyciu arkuszy kalkulacyjnych typu Excel. Wszystko to ma jeden cel – łatwe porównanie efektywności strategii i inwestycji różnego rodzaju.
CAGR
To podstawowa miara zysku/straty używana nie tylko w systemach automatycznych ale również w prezentacjach funduszy inwestycyjnych lub po prostu podsumowaniach przedsięwzięć biznesowych.
Rozwinięcie skrótu: Compound Annual Growth Rate czyli średnioroczna stopa wzrostu. Czasem potocznie używa się jako synonimu – składana stopa wzrostu.
Najprościej rzecz ujmując jest to stopa przyrostu/spadku kapitału inwestycyjnego, liczonego w odniesieniu do wartości początkowej, i wygładzonego do rocznych okresów. Wygładzonego dlatego, że liczy opłacalność inwestycji w taki sposób, jakby co roku ów wzrost/spadek odbywał się z jednakową prędkością, o jednakowy procent, mimo że realnie taka jednorodna stała zmiana jest rzadko możliwa. Nie zawsze w programach testujących systemy jest ona zapisana jako CAGR, np. z tego co widzę Amibroker podaje ją jako CAR ale sposób liczenia jest zawsze ten sam:
Dzielimy wartość końcową inwestycji przez wartość początkową, po czym wynik dzielenia podnosimy do potęgi 1/liczba lat inwestycji i od powstałej kwoty odejmujemy 1. Na koniec mnoży się ją jeszcze przez 100 by uzyskać wynik w procentach.
Przykład:
Wartość początkowa = 10 000 PLN
Wartość końcowa = 25 000 PLN
Lat inwestycji = 5
CAGR = [ (25 000/ 10 000) ^ (1/5) – 1] x 100 = 20,11 %
Inwestując kwotę 10 000 PLN przez 5 lat i uzyskując co roku stopę zwrotu 20,11% oraz reinwestując co roku zysk otrzymamy 25 000 PLN.
W dostępnych w sieci kalkulatorach ale też i w raportach systemowych liczy się CAGR również z niepełnych lat trwania inwestycji. Jeśli np. okres inwestowania trwa 2 lata i 8 miesięcy to program dokonuje przeliczeń tak by wygładzić to do stopy rocznej.
DD (drawdown) i maxDD (max drawdown)
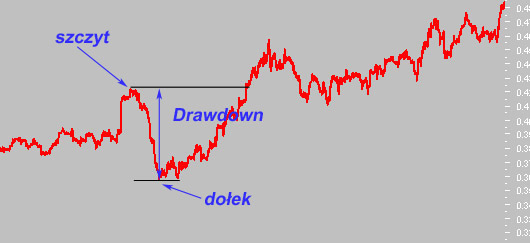
Drawdown to pojedynczy, procentowy spadek jaki zanotowała inwestycja w czasie jej trwania od ostatniej, szczytowej wartości kapitału (w systemie wartość kapitału to tzw. equity) do następującej po niej wartości najniższej, dołka. Drawdownów powstaje w procesie inwestowania wiele ale tylko jeden nazywa się maksymalnym spadkiem (maxDD) – to ten drawdown (zjazd kapitału) o największej wartości pośród nich. Drawdown kończy się wówczas gdy wartość kapitału wraca i przekracza swój poprzedni szczyt. Dla zobrazowania rysunek ukazujący pojedynczy drawdown (pionowa strzałka o 2 ostrzach), czerwona krzywa to linia kapitału (equity) liczona dzień po dniu.
Istotne jest to, że jako maksymalny spadek (maxDD) liczy się nie nominalny ale procentowy zjazd kapitału. Jeśli na przykład od ostatniego szczytu kapitału na poziomie 10 000 PLN doznajemy obsunięcia o 1 000 PLN to stanowi on 10% kwoty wyjściowej. Natomiast jeśli po kilku latach nasz kapitał urasta do 100 000 PLN i zaatakuje nas okresowy spadek o wielkości 5 000 PLN (nominalnie większy od poprzedniego) to jest on równorzędnością 5% obsunięcia od ostatniego szczytu kapitału. A więc to ten pierwszy będzie naszym maxDD o ile nie przydarzy się po drodze jakiś większy niż 10%.
MAR (lub MAR ratio)
Rozwijając ów akronim posłużę się książką Curtisa Faitha ponieważ pojawiały się najróżniejsze interpretacje. Skrót pochodzi od nazwy firmy: Managed Account Ratio LLC, która prowadzi rankingi funduszy hedge i wydaje magazyn na ten temat (http://www.marhedge.com/). Nie ma jednak niejasności jeśli chodzi o liczenie tego współczynnika.
Wystarczą do tego oba mierniki opisane wyżej.
MAR = CAGR % / maxDD %
Dzielimy po prostu procentową, średnioroczną stopę wzrostu, przez najwyższy procentowy spadek kapitału zanotowany w trakcie testu czy realnej inwestycji.
Przykład
CAGR % = 30 %
MaxDD % = 20 %
MAR = 30% / 20% = 1,5
Wartość MAR powyżej 1 uważana jest za dobry wynik. Ale już poziom 2, 3 lub wyżej w długim okresie to naprawdę mistrzostwo jeśli chodzi o akcje czy derywaty.
Dla uświadomienia sobie owej wielkości załóżmy, że kupujemy indeks WIG20 pierwszego dnia jego notowań, za kwotę 100 000 PLN i trzymamy taki portfel bez zmian do dziś. MAR za ten 14 letni okres wyniósł:
MAR = 7,71% / 60,10 % = 0,13
Dla KGHM takie same założenia: MAR= 14,30% / 70,06 % = 0,20
Dla jednostki funduszu PIONEER AP FIO : MAR = 12,48 % / 43,91% = 0,28 %
Ale w przypadku funduszu nie jest to do końca miara precyzyjna. Zresztą sam MAR pomimo swej popularności ma też pewne wady. O tym w kolejnym wpisie.
–* Kathay *–

22 Komentarzy
Dodaj komentarz
Niezależnie, DM BOŚ S.A. zwraca uwagę, że inwestowanie w instrumenty finansowe wiąże się z ryzykiem utraty części lub całości zainwestowanych środków. Podjęcie decyzji inwestycyjnej powinno nastąpić po pełnym zrozumieniu potencjalnych ryzyk i korzyści związanych z danym instrumentem finansowym oraz rodzajem transakcji. Indywidualna stopa zwrotu klienta nie jest tożsama z wynikiem inwestycyjnym danego instrumentu finansowego i jest uzależniona od dnia nabycia i sprzedaży konkretnego instrumentu finansowego oraz od poziomu pobranych opłat i poniesionych kosztów. Opodatkowanie dochodów z inwestycji zależy od indywidualnej sytuacji każdego klienta i może ulec zmianie w przyszłości. W przypadku gdy materiał zawiera wyniki osiągnięte w przeszłości, to nie należy ich traktować jako pewnego wskaźnika na przyszłość. W przypadku gdy materiał zawiera wzmiankę lub odniesienie do symulacji wyników osiągniętych w przeszłości, to nie należy ich traktować jako pewnego wskaźnika przyszłych wyników. Więcej informacji o instrumentach finansowych i ryzyku z nimi związanym znajduje się w serwisie bossa.pl w części MIFID: Materiały informacyjne MiFID -> Ogólny opis istoty instrumentów finansowych oraz ryzyka związanego z inwestowaniem w instrumenty finansowe.


Takie pytanie, może głupie ale jednak. Jeżeli przyjąć Car/Maxdd% jako miarę stabilności systemu. Odnosząc się do "Ale już poziom 2, 3 lub wyżej w długim okresie to naprawdę mistrzostwo." Co należy przyjąć za długi okres? Tzn. nie spodziewam się jednoznacznej odpowiedzi, ale często mam wątpliwości właśnie odnośnie tego jakie przyjąć tutaj założenia. Czy car/maxdd% = 3 dla 2 lat można jakoś porównać do wartości 2.5 dla 8 lat? Może jakieś praktyczne wskazówki? Na oko widać że z reguły odchylenia equity od średniego zysku mają niewiele wspólnego z rozkładem normalnym więc często nie jestem pewien jakie przyjąć założenia.
Proponuję jeszcze zawsze podawać liczbę transakcji, ponieważ moim zdaniem decyduje ona o potencjale systemu.
Jeżeli system generuje dużo transakcji, to jest moim zdaniem bardziej wiarygodny (większe prawdpodobieństwo uzyskania wartości oczekiwanej).
Pozdrowienia,
GiełduGiełdu
Tak dla ścisłości to:
CARG liczony podanym wzorem byłby = [ (10 000/ 25 000) ^ 1/5 – 1] x 100 = -16,74 %
Powinno być , jak mniemam:
CARG = [(10 000/25 000)^(-1/5) -1] x 100 = 20,11 %
pzdr JO
Niestety tak liczony MAR jest niezbyt użyteczny, bo dla CAGR 10%/maxDD 10% i CAGR 40%/maxDD 40% wynik jest ten sam, a faktycznie w drugim przypadku obsunięcie jest dodkliwsze. Ja zamiast niego stosuję współczynnik równy = -log(1 CARG%)/log(1 maxDD%)
korekta: =-log(1-maxDD)/log(1 CARG)
@ ogryzek:
ten drugi jest o niebo lepszy
Do liczenia stopy zwrotu wolę wzór:
=EXP((365-1)*(REGEXPP(X1:X3535;A1:A3535)-1))-1
gdzie kolumna A zawiera datę, a X kapitał.
Jest bardziej odporny na obsunięcie pod koniec testu (zwłaszcza przy silnym lewarowaniu).
Mam prośbę, czy mógłby Pan kiedyś opisać swoje doświadczenia z poziomami DiNapoli’ego, ewentualnie poziomami fibonaciego. Natknąłem się ostatnio na dyskusję, na grupie futures dyskredytująca tę postać, a właśnie zacząłem czytać jego książkę. Może nie warto?
CAGR = [wartość końcowa / wartość początkowa] ^ [1 / liczba lat] -1 !!!
poprawcie sobie tego gifa na bossie 🙂
@Mariusz Tasarz: słuszna uwaga 🙂
@Kathay: dzięki 😉 Bardzo przydatny i poza tym drobnym błędem, jasno napisany tekst.
wzór w wyliczeniach oczywiście niezamierzenie tak wyszedł, juz poprawiam i dzięki!
używam kalkulatora gdzie najpierw podaje się kwotę początkową i tak utkwiło w pamięci 🙁
dzieki również za inne propozycje !
ja również uważam MAR za mało doskonały ale perfekcyjnego po prostu nie ma – dlatego w testach podaje się zwykle całą litanie mierników; nieco lepszy jest R-cube bo stabilniejszy, zrobię w kolejnym wpisie
@Mateusz
Uważam metody DiNapolego za zbyt subiektywne ale oczywiscie postaram się w wolnej chwili opisać dlaczego; to nie znaczy, że złe, być może ktoś poza nim może się w tym wyspecjalizować. Nie pamiętam czy w książce czy na wykładzie Dinapoli sam stwierdził, że tego się nie da zakodować i to jest plus wg. niego. Może i tak ale wszędzie tam gdzie trzeba samemu coś ocenić to mozliwość wpadki rośnie.
Na jego wykładzie tylko jedna rzecz mi się podobała. Wypisał na tablicy wszystkie zniesienia Fibonacciego po czym wszystkie oprócz 2 skreślił mówiąc, że nie działają 🙂 Na pewno zostawił to 50%
TO ALL:
pod poprzednimi wpisami na naszych blogach kwitnie życie gdyby kogoś to interesowało; być moze w jednej z kolejnych wersji blogów będzie widać ostatnie komentarze co ułatwi nawigację
To może napisz jeszcze jak manipulować tymi wskaźnikami w zależności od tego, czy chce się wykazać, że dany system jest dobry do gry lub nie, ewentualnie aby poprawić sobie samopoczucie.
Szef pewnie zajęty, to ja spróbuję podpowiedzieć, jak poprawić wynik żeby się nie stresować niepotrzebnie:
CAGR jest teoretycznie bardziej obiektywny i aby go poprawić najlepiej po prostu obniżyć wartość początkową kapitału.
Przy MAR są trochę większe możliwośći: Najpierw należy zmniejszyć %MaxDD. Robi się to poprzez odpowiednie dobranie początkowej daty testu tak, aby system miał na początku dobry okres wzrostu zyskowności(equity). Po takich zabiegach można mieć super system z CAGR 30% i MAR 3, mimo iż np. od dwóch lat system może generować straty.
@Jacek – Jasne, ale to tylko przy założeniu że nie reinwestujesz zysków. Właściwie w takim wypadku te wskaźniki nie mają znaczenia, a Maxdd jest sens liczyć w takiej sytuacji wyłącznie w wartości nominalnej a nie procentowej.
> Maxdd jest sens liczyć w takiej sytuacji wyłącznie w wartości nominalnej a nie procentowej.
dokładnie tak
Nie ma idealnych mierników !
Moim zadaniem było przybliżenie tych często używanych.
Liczenie maxDD nominalnie nie rozwiązuje żadnego problemu.
Ocena jednej miary ryzyka zwykle nie ma wiekszego sensu. Tak jak podawanie przez fundusze, czy programy inwestycyjne ze mamy wskaznik Sharpe’a (albo dowolny inny) na poziomie 4.
Ocena powinna byc calosciowa. Ale uwzgledniajaca jak najwieksza liczbe wskaznikow, ktore naszym zdaniem dobrze opisują cały „organizm”. Wazne przy tym, by nie powielac kolejnych „pochodnych” wskaznikow, ktore nic nowego juz nie wnoszą.
>Liczenie maxDD nominalnie nie rozwiązuje żadnego problemu.
Jak to nie ?
przynajmniej wiem ile mogłem stracić na jednym kontrakcie.
Jeśli dodam do tego ok 20-30% to z dużym prawdopodobieństwem
wiem jaki będzie następny maxDD.
To procentowy max DD niczego nie rozwiązuje, bo nikt nie gra
danym systemem od początku. Jeśli jak pisałeś wcześniej
ktoś przeznaczy na jeden kontrakt 10 tys. zł i teraz przystąpi do gry
to co mu po %maxDD liczonym od roku 2004, czy 1998 ?
Poza tym często jest tak, że nawet dobry system może mieć na początku
większy spadek zyskowności i będzie to rzutowało cały czas na ten cały %maxDD.
Coś mi się zdaje, że teoria z praktyką nie idą tu w parze 🙂
A ogólnie to moim zdaniem wszystkie te wskaźniki typu MAR,
SharpeRatio, K-Ratio itp. to taka systemowa AF.
AT, którą preferuję to wykres equity.
testy gdy rynek oscylowal wokol 1000 wykazaly 5 strat po rzad przy stoploss 5% czyli 5%*1000*10*5 = 2500 kwotowo obsuniecia. Dla 10k kapitalu poczatkowego jest to 25%mxDD.
w realu gdy zaczynasz grac rynek oscyluje wokol 2000, notujesz 8 strat po 5% czyli masz 5%*2000*10*8 = 8000 kwotowo obsuniecia. Dla 10k kapitalu poczatkowego jest to 80%mxDD.
Wyniki kwotowe(nominalne) nie sa w zadnym stopniu reprezentatywne w dluzszym okresie bo porownujesz rynki na roznych levelach przy roznych poziomach zmiennosci. Testy dla jednego kontraktu z tego wlasnie powodu rowniez – IMHO – nie niosa za soba wiekszej wartosci prognostycznej, jakkolwiek teoretycznie by to nie brzmialo 🙂
>czyli masz 5%*2000*10*8 = 8000 kwotowo obsuniecia. Dla 10k kapitalu poczatkowego jest to 80%mxDD.
właśnie tyle obsunięcia ma obecnie system opisywany we wcześniejszym wątku przez KatHaya.
dokładnie jest to -854 pkt, czyli – 8540 zł na jednym kontrakcie.
Dla rozpoczynającego grę z kapitałem początkowym 10k jest to bankructwo,
ale dla systemu jest tylko -25% maxDD, czyli operacja się uda, ale pacjent jej nie wytrzyma
chociaż w żadnym wypadku nie będzie to "reprezentatywne".
jezeli rozpoczynajacy gre bedzie znal zasady zarzadzania ryzykiem i zauwazy, ze teraz w kazdej transakcji ryzykuje srednio 2000*5%*10 =1000zl, a podczas testu "ryzykowal" 1000*5%*10 =500zl to moze np uzna, ze do gry 1 kontraktem potrzebuje 2 razy wiecej kapitalu niz wczesniej(zeby utrzymac ryzko na podobnym poziomie) i wtedy maxDD w realu wyniesie 40%(=8k/20k) co juz nie bedzie takie nieoczekiwane …
Pingback: Blogi bossa.pl » Blog Archive » Porównywanie systemów mechanicznych, część 4