Oceniając wizualnie korelację pomiędzy stopami zwrotów dwóch instrumentów czy strategii bardzo łatwo ulec złudzeniu.
Co tak naprawdę znaczy hasło: nieskorelowane lub mocno skorelowane stopy zwrotu (2 systemów, strategii, funduszy itd)?
Współczynniki korelacji dwóch zmiennych mieszczą się w przedziale od (-1) czyli idealnie ujemna korelacja do (+1) czyli zupełnie dodatniej korelacji pomiędzy nim, z zerem (0) pośrodku, które oznacza brak jakiejkolwiek korelacji.
Sugestywnie prezentuje to J.Schwager w swojej ostatniej książce, którą już anonsowałem wcześniej: „Market sense and nonsense”. Poniższe 2 diagramy zaczerpnięte stamtąd pokazują porównanie procentowych, miesięcznych zmian stóp zwrotu dwóch funduszy: A i B, na tle indeksu S&P500. Schwager proponuje na ich podstawie takie zadanie z szacowania :
zmiany stóp zwrotu którego z tych dwóch funduszy są bardziej skorelowane ze stopami zwrotu indeksu?
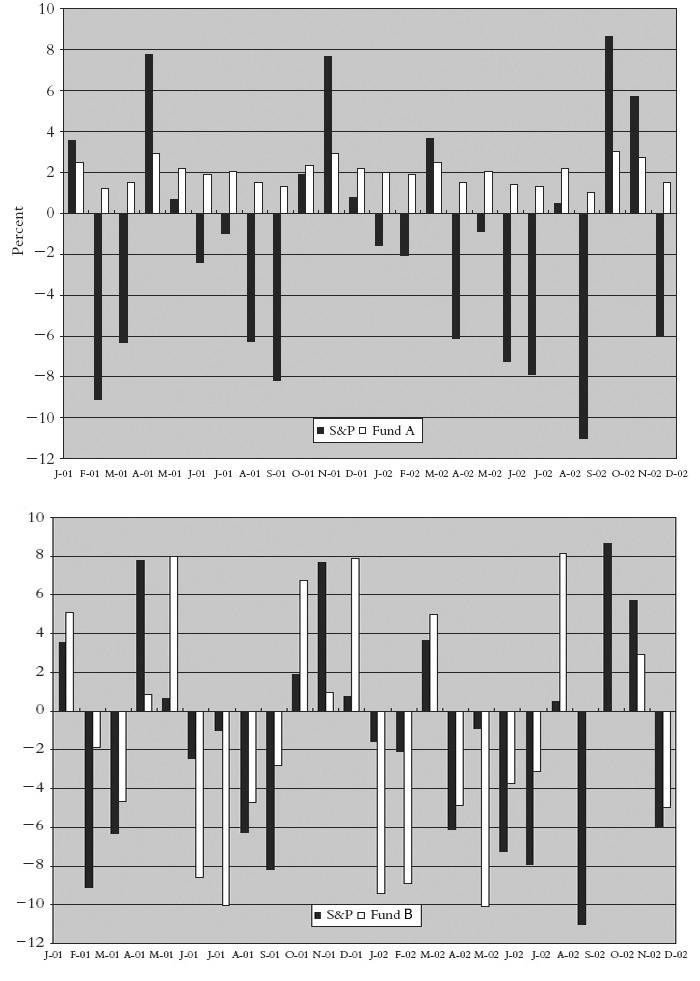źródło: J.Schwager „Market sense and nonsense” (robiąc rysunek do wpisu musiałem poprawić błąd ponieważ w oryginale jest podane dwukrotnie „Fund A” podczas gdy kwestia dotyczy dwóch różnych funduszy A i B)
Pomimo tego, że fundusz A (rysunek górny) notuje tylko zyski, podczas gdy indeks w niektórych miesiącach tracił, to współczynnik korelacji stóp zwrotu w tym przypadku jest wyższy i wynosi 1. Jeśli się dobrze przypatrzyć poszczególnym zmianom to widać, że wzrostowi stopy zwrotu funduszu A odpowiada jednoczesny wzrost stopy zwrotu indeksu, a spadek-spadkowi.
Na rysunku dolnym współczynnik korelacji wynosi tylko 0,41 dla funduszu B. Nietrudno dostrzec gołym okiem, że wycena owego funduszu rośnie zawsze gdy rośnie indeks a spada gdy i indeks spada, jednak same zmiany stopy zwrotu z miesiąca na miesiąc nie synchronizują się w cyklu spadek-wzrost.
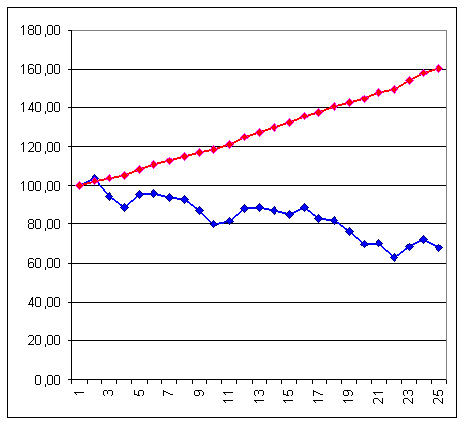
Wizualna inspekcja wykresów może być więc zawodna. Jeśli słyszymy, że stopy zwrotu dwóch instrumentów są idealnie skorelowane dodatnio to nie będzie oznaczać, że krzywa zmian ich cen (trend, tendencja) będzie poruszać się w tym samym kierunku. Widać to na poniższym rysunku, który stworzyłem przez kumulowanie kolejnych stóp zwrotu funduszu A i indeksu S&P500, biorąc szacunkowe wartości właśnie z diagramu wyżej i zaczynając od wspólnego poziomu 100:
———————————————————————————–
I pytanie do konkursu, którego szczegóły we wpisie Michała:
Na czym polega zjawisko „momentum” (impetu) na rynku akcji i podstawowa, dwukierunkowa strategia inwestycyjna wykorzystująca je?
Powodzenia!
—Kat—-
40 Komentarzy
Dodaj komentarz
Niezależnie, DM BOŚ S.A. zwraca uwagę, że inwestowanie w instrumenty finansowe wiąże się z ryzykiem utraty części lub całości zainwestowanych środków. Podjęcie decyzji inwestycyjnej powinno nastąpić po pełnym zrozumieniu potencjalnych ryzyk i korzyści związanych z danym instrumentem finansowym oraz rodzajem transakcji. Indywidualna stopa zwrotu klienta nie jest tożsama z wynikiem inwestycyjnym danego instrumentu finansowego i jest uzależniona od dnia nabycia i sprzedaży konkretnego instrumentu finansowego oraz od poziomu pobranych opłat i poniesionych kosztów. Opodatkowanie dochodów z inwestycji zależy od indywidualnej sytuacji każdego klienta i może ulec zmianie w przyszłości. W przypadku gdy materiał zawiera wyniki osiągnięte w przeszłości, to nie należy ich traktować jako pewnego wskaźnika na przyszłość. W przypadku gdy materiał zawiera wzmiankę lub odniesienie do symulacji wyników osiągniętych w przeszłości, to nie należy ich traktować jako pewnego wskaźnika przyszłych wyników. Więcej informacji o instrumentach finansowych i ryzyku z nimi związanym znajduje się w serwisie bossa.pl w części MIFID: Materiały informacyjne MiFID -> Ogólny opis istoty instrumentów finansowych oraz ryzyka związanego z inwestowaniem w instrumenty finansowe.
„źródło: J.Schwager „Market sense and nonsense” (robiąc rysunek do wpisu musiałem poprawić błąd ponieważ w oryginale jest podane dwukrotnie „Fund A” podczas gdy kwestia dotyczy dwóch różnych funduszy A i B)”
Kathay jestes pewien ze dobrze wybrales 😀 ?
książkę, przykład, czy co innego ? 🙂
Warto jeszcze dodać ,że sama korelacja to tez pewien rodzaj średniej 🙂
Ta sama wysoka wartość korelacji nie oznacza tożsamości przebiegu wykresu.
en.wikipedia.org/wiki/File:Anscombe’s_quartet_3.svg
i coś dla „bystrzaków” jakem nie chwaląc sie sam jestem 🙂
Zwłaszcza 2 przykład przyda sie spekulantom.
mathsisfun.com/data/correlation.html
ok ok (literki) za szybko pisze za wolno mysle
ale policz prosze korelacje na 2 rysunku, ujemna nie ?.. dokonalem tego wizualnie 😉
„Oceniając wizualnie korelację pomiędzy stopami zwrotów dwóch instrumentów czy strategii bardzo łatwo ulec złudzeniu.”
Może być i tak, ale to zależy od tego kto i jak patrzy, no i jaka jest konkretna sytuacja, albowiem na oko to chłop w szpitalu umarł
więc niekumaci łatwo mogą ulec tzw „xzłudzeniu aptecznemu”, jak to ujmował nieodżałowany Wiech (ciekawe czy małolaty wiedzą dziś kto on zacz?).
Jednak w danym przypadku (diagram 1 ) nie ma żadnych problemów i wątpliwości co do ogólnej oceny charakteru i siły korelacji.
Trochę gorzej jest w drugim przypadku, ale od biedy da się, oczywiście jak jak się wie co to jest ta ta cała „koleracja” no i co z niej wynika.
Właśnie, no bo „Co tak naprawdę znaczy hasło: nieskorelowane lub mocno skorelowane stopy zwrotu (2 systemów, strategii, funduszy itd)?”
Otóż korelacja (współzależność cech) określa wzajemne powiązania pomiędzy wybranymi zmiennymi w oparciu o dwa parametry (cechy)
kierunek oraz siłę wartości zmiennej (i ich zmian mierzone względem odpowiednich średnich).
Korelacja liniowa dodatnia pokazuje, że wzrostowi wartości jednej cechy towarzyszy wzrost średnich wartości drugiej cechy zaś korelacja ujemna odwrotnie, informuje że wzrostowi wartości jednej cechy towarzyszy spadek średnich wartości drugiej cechy.
W przypadku pierwszego diagramu sprawa jest więc oczywista, gdyz widać że zawsze spadkowi towarzyszy spadek a wzrostowi wzrost stopy wwrotu, w mniej wiecej podobnek skali co oznacza co najmniej silną korelację.
Wpółczynnik korelacji jest zaś miarą wspomnianej współzależności między dwoma zmiennymi losowymi. Istotność korelacji określa się na podstawie siły związku korelacyjnego.
Przyjmuje się, że jego wartość (bezwzględna) poniżej 0,4 oznacza słabą korelację, od 0,4- do 0,7 średnią korelację, od 0,7-0,9 silną korelacją, zaś powyżej 0,9 bardzo silną współzalezność.
Jednak uwaga – są jest to ujęcie umowne, które może nas wprowadzić w błąd albowiem sam wspóczynnik korelacji ma oganiczoną wartość poglądową i może zmylić, jak się nie wię co jest grane.
W celu usyskania własciwego poglądu co do wpływu na podstawie wyliczonego współczynnika korelacji obliczasie tzw. wskaźnik (wspołczynnik) determinacji liniowej (R2 – wspołczynnik korelacji do kwadratu). Przyjmuje on wartości z przedziału 0- 1 i informuje nas o tym jaka cześć (procent) zmienności zmiennej objaśnianej jest wyjaśniana przez zmiennośćwartości zmiennej objaśniającej.
Przykładowo, załóżmy ze w przypadku diagramu 1 mielibysmy współczynnik korelacji 0,7 – czyli korelację klasyfikowaną jako silną współzależność cech zaś dla diagramu 2 – 0,416 czyli ledwie średnią współzależność.
Tymczasej jak się policzy współczynniki determinacji to wyjdzie nam odpowiednio 0,49 w pierwszym przypadku i ledwie 0,168. Tak więc w pierwszym przypadku widać że inne czynniki niż domniemane mają de facto większy wpływ, mimo że mamy do czynienia z rzekomo „silną korelacją”. Natomiast w drugim przypadku widać, że dopasowanie jest bardzo słabe.
Tak więc ze Schwag(ie)rem, jak to ze szwagrem, można się napić i mecza obejrzeć i pogadac o czarodziejach i czarnoksięznikach, bo on jes z krainy Oz, natomiast dopiero z Lessem można się i napić i pogadać o korelacji, mimo że wzrok ma już nie ten (co dawniej). 🙂
PS
No i proszę zamiast doczytac do końca i odpowiedziec na pytanie o momentum (bo znam, a jakże) to dostałem takiego impetu w odpowiedzi na wpis o korelacji, że zanim doszedłem do końca tekstu to już widzę, że nalezna mi nagroda przeszła mi koło nosa, wielkim pedem! 🙂
Emot miał być oczywiście taki :(, no bo czy jest się z czego cieszyć?
@Less
„..korelacji ma oganiczoną wartość poglądową i może zmylić, jak się nie wię co jest grane.”
Ja bym to określił: jak sie nie wie na czym sie stoi.
Można wtedy fruwać z korelacja jak wolna gołębica i przekonać się ,że relatywizm dla naszego portfela nie jest wskazany.
Niektórzy twierdzą ,że w życiu też.
@darkh
nie liczyłem 2 korelacji 🙂 sprawdzałem jedynie pierwszą w arkuszu dla pewności
@less
już za sam fakt robienia swojego wpisu pod każdym niemal naszym wpisem powinien kwalifikować cię na nagrodę 🙂 Jak to się wyraża w nowomowie: złożę stosowny wniosek u władz 🙂
@pit
Pewnie z dziwadeł korelacyjnych można by fajną książkę stworzyć:)
Ja wybrałem akurat korelację stóp zwrotu ponieważ jeden z naszych funduszy quant niedawno twierdził, że opiera się na nieskorelowanych stopach zwrotu, co wcale nie musi oznaczać to co większość myśli, jak pokazują rysunki powyżej.
Tak na marginesie – Schwager bardzo nieprecyzyjnie robi opisy:( Powyższe diagramy deklarował jako „korelacja funduszu z indeksem” co nie jest tym samym co „korelacja stóp zwrotu funduszu i indeksu”. Ale sama książka inspirująca i ciekawa.
P.s. Do wszystkich, którzy mnie pytają o odpowiedź z KNF:
nie ma jeszcze i na pewno jak tylko dojdzie natychmiast wrzucę do bloga!
I jeszcze o jednej (nie)korelacji:
W USA trwa „index new all time high” party a my tylko się oblizujemy 🙁
Bo u nas nie drukują wystarczająco mamony, która ciągnie rynek 🙂
Nudne jest czytanie nawet samych nagłówków czy szczyt zasłużony, dlaczego nie ma pokrycia w fundamentach (naprawdę? o rany!), dlaczego powinien rosnąć albo jak wolą inni spadać itd. Who cares?! Jeśli znam swoje ryzyko to całe to gdybanie funta kłaków nie warte 🙂
@Less
Pesymistycznie podchodzisz do życia. Wyślij poprawną odpowiedź to sprawdzisz czy Cię ominęła nagroda czy nie 😉
@mwojciechowski
To chyba tzw deja fu, bo jakoś mi się wydaje, że gdzieś coś w podobie już słyszałem. Coś jakby = marudo kup wreszcie ten lis?
Gdzie jest najbliższa kolektura, może kto powie? 😉
Korelacja stóp zwrotu może być przecież ujemna jeśli tylko w okresie szybszego wzrostu wartości jednego aktywa drugie się wlecze i vice versa. Korelacja między samymi wartościami bardziej odpowiada temu co widać „na oko”.
@nmirek
„Korelacja stóp zwrotu może być przecież ujemna jeśli tylko w okresie szybszego wzrostu wartości jednego aktywa drugie się wlecze i vice versa.”
Cos mi się wydaje, że jednak jest wicek rewersal. Jeśli oba aktywa rosną llub spadają ( z tym że jedno szybciej a drugie wolniej) to korelacja powinna być dodatnia.
Na rozum a nie na oko.
(1) Łopatologicznie: korelacja, to zależność pomiędzy odchyleniami od średniej. Wsp. korelacji = 1 oznacza, że odchyleniu o 1 sigma powyżej średniej stopy zwrotu funduszu towarzyszy odchylenie o 1 sigma powyżej średniej stopy zwrotu indeksu. Wsp. korelacji jest ujemny, gdy stopie zwrotu funduszu powyżej średniej towarzyszy stopa zwrotu indeksu poniżej średniej i vice versa.
(2) Jeżeli zmienne są niezależne to ich wsp. korelacji = 0. Nie działa to jednak w drugą stronę, tj. wsp. korelacji = 0 nie oznacza, że zmienne są niezależne. Wsp. korelacji Pearsona dotyczy bowiem wyłącznie zależności liniowej, nie uwzględnia nieliniowych. Łatwo się o tym przekonać: wsp. korelacji Pearsona dla dwóch zmiennych x i y, gdzie y=x^2, pozostających więc w 100% zależności, wynosi 0.
(3) „Wizualna inspekcja wykresów może być więc zawodna” – niekiedy charakterystyka statystyczna jest zawodna, a punktem wyjścia powinna być graficzna reprezentacja. Dobrze ilustruje to tzw. kwartet Anscombe’a:
http://pl.wikipedia.org/wiki/Kwartet_Anscombe%27a
Taleb bywa skrajny w wygłaszanych przez siebie poglądach, ale coś w tym jest: „Anything that relies on correlation is charlatanism”.
@pit65
Właśnie zorientowałem się, że w zasadzie powieliłem twój wcześniejszy komentarz.
” Łatwo się o tym przekonać: wsp. korelacji Pearsona dla dwóch zmiennych x i y, gdzie y=x^2, pozostających więc w 100% zależności, wynosi 0.”
e tam..
http://i.imgur.com/8dJ541k.png
@darkh
Kpisz czy o drogę pytasz? 🙂
chyba kpie 😉
@investor_ts
Nie zaszkodzi.
To jest bardzo poglądowe jak od strony takiej samej formuły matematycznej może powstac tak wiele róznych rzeczywistości .
A niektórzy uważają zwłaszcza w ekonomii ,że jak poznają równanie to lepsza rzeczywistość bedzie sie układac po ich myśli i częstuja tym naiwnych.
@darkh
x symetrycznie względem 0
@investor_ts
„Jeżeli zmienne są niezależne to ich wsp. korelacji = 0.”
?
@lesserwisser
„Jeśli oba aktywa rosną lub spadają ( z tym że jedno szybciej a drugie wolniej) to korelacja powinna być dodatnia.” – możesz nie wprowadzać ludzi w błąd? Mam nadzieję, że nie pisałbyś tych dyrdymałów gdybyś kiedykolwiek widział wzór na wsp. korelacji.
@darkh
Mój excel liczy jakoś inaczej ;):
http://i.imgur.com/DpMHYQk.jpg
@blackswan
Jeżeli zmienne są absolutnie niezależne (nie występuje jakakolwiek zależność), to wsp. kor. = 0.
Jeżeli zmienne są zależne, ale w sposób nieliniowy, to wsp. kor. = 0.
Zatem jeśli ktoś na podstawie wsp. kor. = 0 ogłasza niezależność, to nie jest to do końca prawda. W takim przypadku możemy mówić o niezależności zdarzeń/zmiennych losowych wyłącznie liniowej. Vide przykład paraboli.
I jeszcze jedno. Spójrz na dwa dolne wykresy z kwartetu Anscombe’a i zobacz jaki wpływ na wsp. kor. mają outliers.
ałaaaaa, gracias
miedzy innymi z korelacja szukam koincydencji na wykresie i sie przerazilem tym zerem 😉
@investor
wiem, że taka jest definicja 😛
po prostu pierwszą rzeczą jaka przyszła mi do głowy po przeczytaniu zacytowanego przeze mnie fragmentu było *spurious correlation*
@ investor ts
„Jeśli oba aktywa rosną lub spadają ( z tym że jedno szybciej a drugie wolniej) to korelacja powinna być dodatnia.” – możesz nie wprowadzać ludzi w błąd? Mam nadzieję, że nie pisałbyś tych dyrdymałów gdybyś kiedykolwiek widział wzór na wsp. korelacji.”
Ależ widziałem, i to dobrze bo w czasach kiedy wzrok jeszcze miałem sokoli, co jednak nie wyklucza tego, że go nie zrozumiałem i/lub zapomniałem go od tamtego czasu.
Jednak, cokolwiek pamiętam, a mianowicie to, że :
1. Współczynnik regresji (Pearsona) jest miarą siły związku prostoliniowego między dwoma cechami mierzalnymi (tzw równanie liniowe regresji).
2. a związek prostoliniowy to taką zależność, w której jednostkowym przyrostom jednej zmiennej ( 0bjasniającej – umownie przyczyny) towarzyszy, średnio biorąc, stały przyrost drugiej zmiennej (objaśnianej – umownie skutku).
3. w związku z tym naturalne jest, że pogladowa i intuicyjna interpretacja współczynnika korelacji jest taka:
a „Współczynnik ten wykorzystywany jest do badania związków prostoliniowych badanych zmiennych, w których zwiększenie wartości jednej z cech powoduje proporcjonalne zmiany średnich wartości drugiej cechy (wzrost lub spadek).”
zsi.tech.us.edu.pl/~nowak/ed/korelacje.pdf
b) współczynnik korelacji p mierzy siłę zależności liniowej miedzy dwiema cechami (tzn. wzrost wartości jednej cechy 0 1 powoduje wzrost drugiej o a, niezależnie od obecnej wartości cechy).
http://agrobiol.sggw.waw.pl/biometria/media//paderewski/Statystyka/wyklad%2010%20korelacja%20i%20regresja.pdf
c) „Znak współczynnika korelacji mówi o kierunku związku: „+” oznacza związek dodatni, tj. wzrost (spadek) wartości jednej cechy powoduje wzrost (spadek) wartości drugiej (związek wprost proporcjonalny). „-” – kierunek ujemny, tj. wzrost (spadek) wartości cechy powoduje spadek (wzrost) wartości drugiej (związek odwrotnie proporcjonalny). Przyjmuje się następujące oceny siły związku (pamiętając o odpowiedniej liczebności próby):”
http://home.agh.edu.pl/~bartus/index.php?action=statystyka&subaction=regresja_i_korelacja
Tak więc nie widzę w tym co napisałem ani małej dyrdy ani dużej dyrdy, panie kolego.
@blackswan
Aha. Ale ‚spurious correlation’ dotyczy chyba innej implikacji:
Nieprawdą jest, że jeżeli wsp. kor. jest większy od 0, to zmienne są bezpośrednio zależne (przyczynowo-skutkowo).
true, implikacja w drugą stronę, my bad
@lesserwisser
Rzuć jeszcze raz okiem na wzór. Co widzisz w liczniku? Średnią wartość iloczynu odchyleń wartości zmiennych OD ICH ŚREDNICH (czyli korelacja to znormalizowana kowariancja). Możemy sobie zatem wyobrazić sytuację, że wzrostowi wartości jednej zmiennej odpowiada wzrost wartości drugiej i vice versa, ale ze względu na średnie wartości zmiennych wsk. korelacji jest ujemny. Zachęcam do poeksperymentowania w Excelu.
Wydaje mi się, że bez założenia rozkładu zmiennych zbliżonego do rozkładu normalnego oraz nieistnienia obserwacji odstających, współczynnik korelacji Pearsona możemy wyrzucić na śmietnik. Życzę zatem powodzenia wszystkim liczącym korelacje na rynkach finansowch 🙂
Zadanie (dla lesserwisser’a)
dwa aktywa dały stopy zwrotu:
x) +5,+4,+3,+2,+1
y) +1,+2,+3,+4,+5
Oblicz korelację stóp zwrotu.
„współczynnik korelacji Pearsona możemy wyrzucić na śmietnik.”
przyszedł i zabrał zabawki ;D
zawsze pozostają correlation swapy itp, gdzie nie tylko wsp. ten nie idzie na śmietnik, ale jest wręcz głownym daniem.
@ blackswan
„zawsze pozostają correlation swapy itp, gdzie nie tylko wsp. ten nie idzie na śmietnik, ale jest wręcz głownym daniem.”
No i czasem tak je miszczowie mass destruction cuisine wypichcą, że wychodzi im zrealizowany współczynnik korelacji na poziomie ponad 1, a wtedy całe pieczołowicie przysządzone danie jest niezjadliwe.
A właściwie to wielce zjadliwie (czytaj jadowite), bo misternie ułożony schemat transakcji z właściwymi parametrami zmiennosci i zalłożoną 100% korekacją, bierze w łeb, czyli mówiąc obrazowo zjada konto z dużym apatytem. 🙂
Przywołuje mi wspomniane zasłyszanej starej historii o słynnym majorze Kuźmie, ze Studium Wojskowego na Uniwersytecie Warszawskim.
Podczas jednego ze szkoleń podobno powiedział on studentom, że podczas strzelania z działa kąt podniesienia lufy, sinus alfa, wynosi 1,5! Na to wstaje jakiś student i mówi – Obywatelu majoprze sinus nie może być większy od 1. A obywatel major na to odpowiada tak, mniej więcej, siadajcie mąadralo i zapamietajcie sobie że w warunkach bojowych wszystko jest możliwe.
Jak widać wcale się nie mylił!
PS
@ All
Dziś wieczorem zamieszcze obszerny komentarz o korelacji, który mam nadzieję podsumuje dotychczasową dyskusję i rozwieje pewne niejasności i wątpliwości.
less
będziesz może na warszawskim spotkaniu bossablo?
blackswan
Nie na dziś trudno powiedzieć, wszystko zależy od tego jak przebiegać będzie moja rekonwalescencja, bo na razie jestem na zwolnieniu lekarskim do końca marca.
less
W takim razie szybkiego powrotu do zdrowia życzę.
Koniecznie daj znać czy wpadniesz – również wpadłbym wypić razem browara i zajrzeć w głąb Twojej duszy 😉
blackie
Dobry browar niezła rzecz, a jak, w dobrej kompanii, będziesz miał okazję zajrzeć mi pod wątrobę to może zobaczysz czemu błędne jest, powszechnie przyjęte, założenie iż w formule wyceny opcji (model binominalny) nie są istotne prawdopodobieństwa zmiany ceny istrumentu bazowego.
Ja to już dawno rozgryzłem, niby prostę a jednak coś! 🙂
@ mirek
„Zadanie (dla lesserwisser’a). dwa aktywa dały stopy zwrotu…”
Wprawdzie nie bardzo wiem gdzie nas ma zaprowadzić to pytanie, ale jednak odpowiadam, że uczony wEksel pokazuje, iż WKP (współczynnik korelacji Pearsona) wynosi tu -1, i nie dziwota.
Jak bowiem uczą nas mądre teksty w przypadku badania korelacji stóp zwrotu, statystyki korelacyjne są miarą zharmonizowania /zgodności / zbieżności kierunków zmian/ruchu stóp zwrotu z dwóch aktywów (comovement lub joint directionality).
W przypadku, gdy korelacja jest liniowa można stwierdzić, iż wartości y wzrastają lub spadają proporcjonalnie (współmiernie) do wzrostu lub spadku wartości x, w tym samym kierunku, tym bardziej zgodnie im wyższa jest korelacja (w wartościach bezwzględnych).
Współczynnik korelacji dwóch szeregów danych uważa się więc za agregatowy wskaźnik podobieństwa tendencji obu szeregów. Jeżeli współczynnik korelacji r(ro/rho) > 0, to oba szeregi charakteryzują się zgodnym kierunkiem zmian, czyli są zharmonizowane ( tym bardziej, im r jest większe dążąc do 1). Jeżeli zaś r < 0, oba szeregi charakteryzują się odmiennymi kierunkiem rozwoju, a więc są niezharmonizowane (i to tym bardziej im r jest bliższe wartości -1).
Dokładniej zaś biorąc to znak plus oznacza że zależność liniowa dodatnia, tzn. wraz ze wzrostem wartości jednej cechy rosną średnie wartości drugiej z cech (zaleznośc liniowa dodatnia), zaś znak minus świadczy, że wraz ze wzrostem wartości jednej cechy maleją średnie wartości drugiej z cech (zależność liniowa ujemna).
To jest tylko opis ogólnej prawidłowości, który uprawniony jest w danym przypadku gdyż dane są tak dobrane że wychodzi nam idealna korelacje ujemną, jednak należy mieć na uwadze że próbka jest o wiele za mała aby wyliczenie było na tyle wiarygodne by przyjąć bez zastrzeżeń występowanie tak silnej korelacji.
Uważa się bowiem, że WKO można, w miarę wiarygodnie przyjmować przy danych powyżej 30 obserwacji (minimum absolutum 25), a najlepiej przy 50 a nawet 100 przypadkach. Poniżej 30 obserwacji zaleca się stosować współczynnik korelacji rang Spearmana (który zasadniczo stosuje się dla przypadków cech jakościowych a nie ilościowych).
@ investor ts
"Rzuć jeszcze raz okiem na wzór. Co widzisz w liczniku? Średnią wartość iloczynu odchyleń wartości zmiennych OD ICH ŚREDNICH (czyli korelacja to znormalizowana kowariancja). Możemy sobie zatem wyobrazić sytuację, że wzrostowi wartości jednej zmiennej odpowiada wzrost wartości drugiej i vice versa, ale ze względu na średnie wartości zmiennych wsk. korelacji jest ujemny. Zachęcam do poeksperymentowania w Excelu."
Niestety, nie będę więcej rzucał okiem na ten wzór bo mam go już dosyć tej całej statystyki. Jakoś nie bardzo mi się jednak chce wierzyć, że tak może być ale nie wykluczam tego (bo nie takie cuda już mnie zaskakiwały), nie będę jednak eksperymentował w Excelu gdyż zostawiam to koledze (i zachęcam to tego), bo jak wyjdzie na jego to oddam cesarzowi co cesarskie, publicznie.
W związku z powyższym mam wątpliwości co do prawidłowości niektórych konkluzji we wpisie Kathaya, o czym później.
"Wydaje mi się, że bez założenia rozkładu zmiennych zbliżonego do rozkładu normalnego oraz nieistnienia obserwacji odstających, współczynnik korelacji Pearsona możemy wyrzucić na śmietnik. Życzę zatem powodzenia wszystkim liczącym korelacje na rynkach finansowch."
Zasadniczo biorąc powyższe uwagi mają swoje uzasadnienia, ale warto chyba trochę szerzej pochylić się nad tymi kwestiami, aby była lepsza jasność w temacie, co zresztą może się przydać czytelnikom na przyszłość.
Faktycznie założenie normalności rozkładu oraz nieliczność i niewielka skala obserwacji odstających (odchyleń od teoretycznej linii regresji linowej) jest tu istotna i pomocna, albowiem z założenia obie zmienne powinny być mierzalnymi zmiennymi ciągłymi z normalnym rozkładem.
Nie będę tutaj ponowie orał już zaoranej działki i pisał coś madrego od siebie, tylko pojdę na łatwiznę i wesprę się , w celach dydaktyczno-ilustracyjnych, obszernymi cytatami z bardzo poglądowego artykułu profesora Bogusława Guzika (statystyka i ekonometryka) pod tytułem "Empiryczne szacowanie zależności ekonomicznych".
Link do artykułu, dostępnego w sieci, poniżej:
www.kpsw.edu.pl/menu/pobierz/RE1/3Guzik.pdf
W artykule tym, który gorąco wszystkim zainteresowanym polecam, omówiono uwarunkowania i ograniczenia stosowania współczynnika korelacji liniowej w ekonomii i co najwazniejsze uczulono na typowe błędy w jego stosowaniu.
Poczytajmy więc i zapamiętajmy (oczywiście po przemyśleniu):
" Ustalanie charakteru powiązań wielkości gospodarczych tylko na podstawie wykresów jest bardzo subiektywne. Na tym samym rysunku jeden analityk dopatrzy się związku silnego, inny słabego, a jeszcze inny żadnego. Może być wreszcie tak, że przy bardzo niestabilnych przebiegach jeden będzie twierdził że powiązanie jest rosnące, drugi zaś że jest malejące. Czytanie wykresów wymaga sporych umiejętności, a ponadto jest procedurą niejednoznaczną.
Wartość współczynnika korelacji jest jednak różnie interpretowana, niekiedy ostrożnie . jako wskaźnik podobieństwa tendencji zmian porównywanych wielkości, ale niekiedy bardzo silnie,. jako miara powiązania badanych wielkości lub wręcz nawet jako miara zależności.
W każdym razie powszechność używania współczynnika korelacji w ekonomii prowadzi czasami do swoistych nadużyć metodologicznych, co omówimy w dalszym ciągu artykułu.
W ekonomii ilościowej postępowanie jest tu niemal szablonowe: liczy się współczynnik korelacji między szeregami danych obu wielkości i przyjmuje się, że ten współczynnik jest wskaźnikiem siły zależności (powiązania) zmiennej Y od zmiennej X.
Otóż zwykły współczynnik korelacji liniowej może być uznany
za wskaźnik siły zależności między zmienną Y (np. popyt) a zmienną X (np. dochody) tylko wtedy, gdy jednocześnie:
1. zmienna X rzeczywiście jest czynnikiem kształtującym zmienną Y, a więc gdy gruntownie zweryfikowana teoria i powszechne przekonanie profesjonalistów wskazują, że Y zależy od X , co znaczy, że X jest przyczyna a Y skutkiem.
Wprawdzie współczynnik korelacji liniowej Pearsona między Y a X jest taki sam jak między X a Y, jednak ekonomista musi rozstrzygnąć, co od czego zależy, a więc musi określić, co jest zmienną zależną a co zmienną niezależną. Ekonomista może interpretować tylko współczynnik korelacji między Y a X.
2. zmienna X jest jedynym czynnikiem oddziałującym na Y lub też w zmiennej X odzwierciedlają sie wszystkie czynniki kształtujące zmienną Y;
3. zależność między zmienną Y a zmienna X jest liniowa.
Tylko w tym przypadku obliczanie standardowych (pearsonowskich) współczynników korelacji można byłoby z całkowitym przekonaniem potraktować jako odgadywanie siły zależności tych zmiennych. Jeśli jednak któryś z podanych trzech warunków nie jest spełniony, przyczynowo-skutkowa. interpretacja współczynnika korelacji jako miernika siły zależności nie jest uzasadniona. To samo dotyczy też interpretacji wykresów tzw. empirycznej zależności, takich jak w paragrafie poprzednim.
W praktyce prawie zawsze nie jest spełniony warunek drugi, gdyż wielkości ekonomiczne zależy na ogół od więcej niż jednej zmiennej niezależnej. Podważa to wiele badań empirycznych, które oparte są na obliczaniu zwykłych współczynników korelacji, nawet jeśli zależność jest przyczynowo-skutkowa oraz liniowa.
Współczynnik korelacji uznawany jest bowiem , "na wyrost", jako miernik siły zależności, podczas gdy określa on jedynie czysto statystyczne podobieństwo kształtowania się zbiorów danych.
Dodajmy, że spotyka się też stwierdzenia całkowicie negujące przydatność współczynnika korelacji, np. poglądy takie, że korelacja to nie zależność., że mierzenie korelacji nie jest mierzeniem zależności. Z tak daleko idącym poglądem też się nie zgadzamy. W pewnych szczególnych przypadkach (zob. założenia 1,2,3 powyżej) współczynnik korelacji jest miernikiem zależności.
Współczynnikowi korelacji nadaje się różne interpretacje. Pomijając (poprawną ) tautologię, że współczynnik korelacji mierzy zależność korelacyjną oraz (poprawne) czysto matematyczne spojrzenie na współczynnik korelacji jako na .parametr populacji wielowymiarowej, czy jako na .miarę podobieństwa dwóch zbiorów liczb, w zasadzie pozostaje tylko jedna, mająca naturę ekonomiczna, interpretacja współczynnika korelacji, mianowicie interpretacja jako miernika
podobieństwa kierunku zmian:
Jeśli porównywane wielkości notowane są w kolejnych momentach czasu, to współczynnik korelacji może służyć do mierzenia podobieństwo tendencji zmian porównywanych wielkości, czyli do mierzenia tzw. podobieństwa kierunku tych wielkości albo, jeszcze inaczej, do określania stopnia zharmonizowania obu przebiegów.
Dodatni współczynnik korelacji oznacza, że obie porównywane wielkości charakteryzowały się podobnymi tendencjami zmian, czyli że wzrostowi jednej towarzyszy, średnio biorąc, wzrost drugiej wielkości lub że spadkowi jednej towarzyszy spadek drugiej (rys. 5), a więc że oba przebiegi były zharmonizowane.
Im dodatni współczynnik korelacji jest bliższy +1, tym większe jest
podobieństwo kierunku zmian.
Ujemny współczynnik korelacji wystąpi natomiast wtedy, gdy tendencje zmian obu porównywanych wielkości były niepodobne: jedna rosła a druga malała, czyli gdy oba przebiegi były niezharmonizowane. Im współczynnik korelacji jest bliższy -1, tym niepodobieństwo kierunku zmian (niezharmonizowanie) jest coraz większe.
Zerowa wartość współczynnika korelacji oznacza, że średnio biorąc .
zmianom jednej wielkości nie towarzyszyły zmiany drugiej wielkości
Co najwyżej jest wskaźnikiem zgodności kierunku zmian badanych wielkości, czyli ich zharmonizowania."
Jak więc widać współczynnik korelacji liniowej Pearsona nie tylko nie jest miarą doskonałą (but nobody is perfect), ba jest miarą statystyczną ułomną, lecz jeśli ma się świadomość charakteru i uwarunkowań tej ułomności i ograniczeń to można uniknąć wielu nieporozumień i błędów przy interpretacji i stosowaniu tego współczynnika zmienności. A błędy te wynikające z niepełnego zrozumienia istoty zagadnienia i/lub niewłaściwego podejścia do niego, zdarzają się dosyć często.
I temu właśnie zabezpieczeniu przed tym ( coś w podobie hedźingu) przyświecało moje pochylenie się nad tym jakże popularnym miernikiem statystycznym. Mam nadzieję że z potencjalnym pożytkiem.
Teraz już uzbrojeni w odpowiednią wiedzę możemy krytycznie (co nie znaczy krytykancko) spojrzeć na to co napisał Szwagier (Piekutoszczak 🙂 a może Kathay.
" Pomimo tego, że fundusz A (rysunek górny) notuje tylko zyski, podczas gdy indeks w niektórych miesiącach tracił, to współczynnik korelacji stóp zwrotu w tym przypadku jest wyższy i wynosi 1. Jeśli się dobrze przypatrzyć poszczególnym zmianom to widać, że wzrostowi stopy zwrotu funduszu A odpowiada jednoczesny wzrost stopy zwrotu indeksu, a spadek-spadkowi.
Na rysunku dolnym współczynnik korelacji wynosi tylko 0,41 dla funduszu B. Nietrudno dostrzec gołym okiem, że wycena owego funduszu rośnie zawsze gdy rośnie indeks a spada gdy i indeks spada, jednak same zmiany stopy zwrotu z miesiąca na miesiąc nie synchronizują się w cyklu spadek-wzrost."
I teraz już nas chyba nie wprowadzi w błąd ani, nie zdziw, to co widzimy na przytoczonych wykresach i będziemy w stanie je właściwie zinterpretować, chłodnym i uzbrojonym ( w wiedzę) okiem świadomego inwestora.
I będziemy wiedzieli, że to iż "same zmiany stopy zwrotu z miesiąca na miesiąc nie synchronizują się w cyklu spadek-wzrost" nie jest istotne z punktu widzenia znaku korelacji (kierunku zmian cech badanych) a ma jedynie wpływ na siłę związku korelacyjnej współzależności (wysokość współczynnika korelacji).
@ kathay
W świetle powyższych uwag mam poważne wątpliwości odnośnie poprawności poniższych konstatacji, być może coś z twoją metodologia liczenia jest nie tak?
"Wizualna inspekcja wykresów może być więc zawodna. Jeśli słyszymy, że stopy zwrotu dwóch instrumentów są idealnie skorelowane dodatnio to nie będzie oznaczać, że krzywa zmian ich cen (trend, tendencja) będzie poruszać się w tym samym kierunku. Widać to na poniższym rysunku, który stworzyłem przez kumulowanie kolejnych stóp zwrotu funduszu A i indeksu S&P500, biorąc szacunkowe wartości właśnie z diagramu wyżej i zaczynając od wspólnego poziomu 100:"
Albowiem, według wszelkich znaków na niebie i ziemi, powinno być tak że jeśli stopy zwrotu dwóch instrumentów są idealnie skorelowane dodatnio to ich ceny powinny poruszać sie w tym samym kierunku.
Przemyśl to proszę i przelicz jeszcze raz.
I to by było na tyle!
@investor_ts
Ha, czyli przegrałbym zakład. Następnym razem nie miej skrupułów i uderzaj w mojego bida – jestem honorowy, zobowiązania reguluję 🙂
@lesserwisser
Miałem nadzieję, że nie spełnisz swojej groźby i nie będziesz usiłował rozwiewać niejasności 😉
„Albowiem, według wszelkich znaków na niebie i ziemi, powinno być tak że jeśli stopy zwrotu dwóch instrumentów są idealnie skorelowane dodatnio to ich ceny powinny poruszać sie w tym samym kierunku.”
Less, dodatnia korelacja stóp zwrotu oznacza – o czym pisze Kathay – że ZMIANY CEN poruszają się ŚREDNIO w tym samym kierunku, a nie CENY. W opisywanym przykładzie cena funduszu A wyłącznie rośnie, ale zmiana cen porusza się średnio zgodnie ze zmianami stopy zwrotu indeksu – stąd dodatnia korelacja.
„nie będę jednak eksperymentował w Excelu gdyż zostawiam to koledze (i zachęcam to tego)”
Zachęcony wykonałem krótkie ćwiczenie:
http://i.imgur.com/5QUtpjP.jpg
Na czym polega „myk” zastosowany przez Schwagera? Zgodnie z tym co pisałem wyżej, dobieramy wartości tak, aby odchylenia poszczególnych wartości zmiennych od ich średnich były równe (licząc w odch. std.)
„Przemyśl to proszę i przelicz jeszcze raz.”
Wszystko się zgadza, a Kathayowi należą się słowa uznania za podejmowanie takich tematów. Bo chociaż nie dojdziemy zapewne do konkluzywnych wniosków, to umożliwiają one weryfikację naszych potocznych, często naiwnych, przekonań.
Pozdrawiam.
Jestem (już), pamiętam (jeszcze),czuwam (wciąż) – a więc wrócę, nie zasmucę! 🙂