W ostatnim (chwilowo ?) wpisie z serii na temat wyboru najefektywniejszego, na własny użytek i pod wieloma kątami widzenia, systemu mechanicznego, pozostało rozłożenie miernika R-Cubed na czynniki pierwsze.
Pełna jego nazwa, nadana przez Curtisa Faitha brzmi:
ROBUST RISK/REWARD RATIO (RRRR)
czyli w luźnym tłumaczeniu ?Stabilny wskaźnik ryzyko/wygrana”.
Trzeba zaznaczyć, że Curtis inspirację do jego stworzenia w dużej mierze zawdzięcza legendarnemu już traderowi – Markowi Johnsonowi, który dla propagowania mechanicznych systemów zrobił bardzo wiele, szczególnie w internecie, warto więc zapamiętać to nazwisko choć on sam występuje zwykle pod wieloma nickami.
R-Cubed jest wynikiem dzielenia przez siebie 2 składników:
1/ RAR% – podstawia się we wzorze do licznika
Opisany w poprzednim odcinku, występuje tutaj jako stabilniejsza miara „zyskowności” systemu niż CAGR, mniej wrażliwa na okresy sporej zmienności linii equity. I powinienem jeszcze dodać dwa szczegóły, nieopisane wcześniej:
a/ponieważ dla zyskownego systemu współczynnik nachylenia regresji liniowej jest ułamkiem i wynosi pomiędzy 0 a 1, dlatego na potrzeby użycia go jako miary zysku mnoży się ów wynik przez 100. Dla nachylenia np 0,35 używa się więc jako RAR% – 35%.
b/ RAR% liczy się de facto dla rocznych zmian krzywej kapitału, jeśli obliczenia wykonujemy dla dziennych zysków/strat to należy otrzymaną wartość przekonwertować do zmiany rocznej.
2/ Mianownik składa się natomiast z 2 komponentów
(I) średniego maksymalnego obsunięcia liczonego w procentach (AMDD – Average Maximum Drawdown)
Aby je obliczyć
– znajdujemy 5 największych procentowych obsunięć, jakie podczas testów doznał badany system
– sumujemy wszystkie obsunięcia i dzielimy wynik przez 5
(II) dopasowania czasowego (AMDDL – Average Maximum Drawdown Lenght)
Aby je obliczyć
– znajdujemy długość średniego maksymalnego obsunięcia;
robimy to znajdując czas trwania (w ilości dni) każdego z 5-ciu największych obsunięć; czas trwania obsunięcia to okres pomiędzy ostatnim szczytem linii kapitału (equity peak) a jego pokonaniem po raz pierwszy po zaliczeniu obsunięcia (new equity high) ; sumujemy owe 5 znalezionych okresów i dzielimy wynik przez 5
– znalezioną długość średniego maksymalnego obsunięcia normalizujemy dzieląc je przez 365 dni
Pełen wzór:
Przykład:
RAR% systemu = 50%
Średnie maksymalne obsunięcie = 25%
Długość średniego maksymalnego obsunięcia = 730 dni
R-CUBED = 50 / (25 * 730/365) = 50 / (25*2)=50/50=1
Poprawione zostało więc kilka wad poprzednich wskaźników. Oprócz mniej wrażliwej miary zysku (RAR%) mamy tutaj:
– 5 maksymalnych obsunięć co niweluje szum przypadkowego, jednego, czasem nienaturalnego i nieproporcjonalnego obsunięcia maxDD
– bierzemy pod uwagę czas wychodzenia ze zjazdów linii kapitału, czego zwykle żaden z mierników nie bierze pod uwagę.
Curtis proponuje również użycie %RAR w mianowniku wskaźników MAR i Sharpe dla większej stabilności. Wówczas wzory wyglądają następująco:
Robust Sharpe = RAR% / Odchylenie standardowe
Robust MAR = RAR%/ maxDD
Na koniec mój skromny komentarz:
Jeśli R-cubed traktujemy jako pomoc na własny użytek w wyborze najlepszego zbudowanego systemu, to nie ma aż takiego znaczenia w jakiej postaci użyjemy jego składowych, byle sposób liczenia był identyczny dla wszystkich backtestów. Nie musi więc być to wersja kanoniczna jak wyżej. Zamiast RAR% nadal możemy użyć dowolnej miary zyskowności, zamiast 5 obsunięć można liczyć 3 czy 10 albo nawet wszystkie. Porównujemy wszak zdolności naszych systemów a nie stajemy w zawodach o wynalezienie perfekcyjnego wskaźnika. Nie jest powiedziane, że w kolejnej wersji TradingBloxa nie wystąpi jakaś modyfikacja R-Cubed. Przybliżenie go tutaj miało za zadanie inspirować do własnych poszukiwań.
Idealny matematyczny miernik systemu transakcyjnego nie istnieje, a na pewno żaden nie mówi za wiele o realnej przyszłości naszych strategii. W świecie niestacjonarności, wybieranie najlepszego systemu pod względem wyników opartych o test danych historycznych jest robotą nieco na wyrost, szacunkiem co najwyżej. Poza tym koniecznie trzeba uwzględnić wszelkie „subiektywne” wskazania, te o podłożu psychologicznym opisane w tym cyklu. Ja zawsze będę jednak zwolennikiem blendowania systemów a więc użycia kilku z nich jednocześnie dla większej dywersyfikacji ryzyka. Nawet jeśli osiągi każdego z nich z osobna nie są porażające, stosowane razem potrafią dać całkiem niewyobrażalny efekt synergii .
—*Kat*—
3 Komentarzy
Dodaj komentarz
Niezależnie, DM BOŚ S.A. zwraca uwagę, że inwestowanie w instrumenty finansowe wiąże się z ryzykiem utraty części lub całości zainwestowanych środków. Podjęcie decyzji inwestycyjnej powinno nastąpić po pełnym zrozumieniu potencjalnych ryzyk i korzyści związanych z danym instrumentem finansowym oraz rodzajem transakcji. Indywidualna stopa zwrotu klienta nie jest tożsama z wynikiem inwestycyjnym danego instrumentu finansowego i jest uzależniona od dnia nabycia i sprzedaży konkretnego instrumentu finansowego oraz od poziomu pobranych opłat i poniesionych kosztów. Opodatkowanie dochodów z inwestycji zależy od indywidualnej sytuacji każdego klienta i może ulec zmianie w przyszłości. W przypadku gdy materiał zawiera wyniki osiągnięte w przeszłości, to nie należy ich traktować jako pewnego wskaźnika na przyszłość. W przypadku gdy materiał zawiera wzmiankę lub odniesienie do symulacji wyników osiągniętych w przeszłości, to nie należy ich traktować jako pewnego wskaźnika przyszłych wyników. Więcej informacji o instrumentach finansowych i ryzyku z nimi związanym znajduje się w serwisie bossa.pl w części MIFID: Materiały informacyjne MiFID -> Ogólny opis istoty instrumentów finansowych oraz ryzyka związanego z inwestowaniem w instrumenty finansowe.

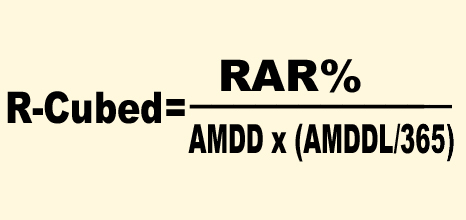

„Ja zawsze będę jednak zwolennikiem blendowania systemów a więc użycia kilku z nich jednocześnie dla większej dywersyfikacji ryzyka. Nawet jeśli osiągi każdego z nich z osobna nie są porażające, stosowane razem potrafią dać całkiem niewyobrażalny efekt synergii .”
Tomaszu wiernie trzymający fason swoich wpisów. Bardzo mądrze piszesz. Bo opieranie się tylko na jednym mierniku jest tak samo głupie jak wybieranie w ramach optymalizacji samotnego najwyzszego szczytu w rozkładzie optymalizowanej zmiennej, gdy obok mamy ładne „wzgorze” pozytywnych wartości, troszkę mniejszych, ale sumarycznie bezpieczniejszych. NIe wiem czy zrozumialem to napisałem, ale chodzi o to by po prostu tak jak mówisz nie opierać się na jednej nodze gdy wiatr hula, sztorm kołysze łajbę i chce nas zmyć z pokładu. Szmata na kiju, bujamy…
Poszukuje algorytmu, który oblicza wartość zniesień linii kapitału. Przy testowaniu systemów korzystam jedynie z excela. Dziekuję za odpowiedzi!
lepiej pytaj na futures.pl