Czy zmienność rynku równa się ryzyku?
Temat co jakiś czas przewija nam się tutaj w anturażu gorących dyskusji, tym razem zbiorę całość zagadnienia do kupy i zilustruję cytatami oraz obrazkami.
To niemal powszechny zwyczaj w branży finansowej, że zmienność rynku utożsamia się z ryzykiem, które ponosi inwestor. Nietrudno trafić na takie właśnie podejście w analizach, komentarzach, pracach naukowych i literaturze. Czy takie traktowanie zmienności, liczonej odchyleniem standardowym, wariancją, ATRem czy inną miarą, jest prawidłowe? Wiem z poprzednich wpisów na ten temat, że Czytelnicy naszych blogów okupują dwa przeciwne obozy opinii w zakresie tego podejścia. Sprawdźmy jak to wygląda w szczegółach w dwóch wymiarach opisanych poniżej.
1. Wymiar praktyczny
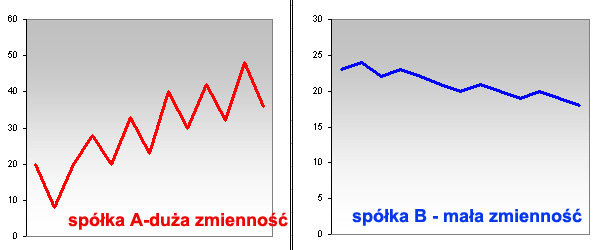
Proszę spojrzeć na poniższe wykresy 2 spółek. Ich dzienne przebiegi kursów różni znacznie właśnie zmienność, co zresztą można dostrzec bez dokonywania obliczeń.
To oczywiście nieco uproszczony obraz, ale oddający problem. Gdyby ryzyko mierzyć właśnie zmiennością to akcje spółki A (po lewej) trzeba by określić jako bardziej ryzykowne, spółki B – jako bezpieczniejsze. Czy rzeczywiście kupno spółki B w dowolnym momencie można określić jako mniej ryzykowną decyzję? Oczywiście przyszła zmienność nie musi opowiadać tej dotychczasowej, ale wybierając inwestycję zwykle kierujemy się zmiennością właśnie zastaną na rynku lub tą z poprzednich okresów.
W innym przykładzie pokazywanym przez mnie w przeszłości kursy w dołku bessy poruszały się z wielką zmiennością, podczas gdy na szczycie kolejnej hossy zmieniały się niewiele. Gdyby czynnikiem ryzyka była zmienność to kupno na owym szczycie należałoby traktować jako dużo bardziej bezpieczną decyzję.
Jak widać łatwo się pomylić szacując ryzyko w oparciu o samą zmienność, w praktyce należałoby więc otrożnie używać obu słów wymiennie lub stawiać między nimi znak równości.
2. Wymiar teoretyczny
Właściwie trudno dziwić się powszechnemu użyciu zmienności jako miary ryzyka gdyż od dziesiątków lat tak właśnie traktują tę zależność instytucje czy naukowcy, w tym Nobliści, tworzący zręby nowoczesnej teorii finansów. W 1952 r. Harry Markowitz w swojej Modern Portfolio Theory definiuje ryzyko jako wariancję od średniej. Podobnie Fama w w swoich hipotezach efektywnego rynku. Burton Malkiel w klasycznej „A Random walk down Wall Street” z 1973 r. objaśnia:
„Investment risk, then, is the chance that expected security returns will not materialize and, in particular, that the securities you hold will fall in price. … Thus, financial risk has generally been defined as the variance or standard deviation of returns.”
(to tłumaczenie i kolejne pochodzą od mnie: “Ryzyko inwestycji w takim razie oznacza możliwość, że oczekiwana stopa zwrotu akcji nie zmaterializuje się oraz w szczególności, że kursy akcji, które posiadasz, spadną… Tak więc ryzyko finansowe generalnie zostało zdefiniowane jako wariancja lub odchylenie standardowe”).
Ale sięgnijmy również gdzieś bardziej współcześnie, do świata quants, w którym Paul Wilmott gra jedne z pierwszych skrzypiec. W swojej książce „Frequently asked question in quantitative finance” podaje on matematyczną definicję ryzyka:
“In finance it refers to the possibility of a monetary loss associated with investments.”
(“W finansach ryzyko odnosi się do możliwości pieniężnej straty na inwestycjach”)
Dodając chwilę dalej:
“The most common measure of risk is simply standard deviation of portfolio returns.” (“Najpopularniejszą miarą ryzyka jest po prostu odchylenie standardowe zwrotów portfela”).
I tak można by cytować w nieskończoność.
Takie podejście to pewne uproszczenie, przydatne do budowy modeli i analiz finansowych. Zakłada ono, że fluktuacje cen instrumentów same w sobie niosą ryzyko (tzw. systematic risk), nie sięga do źródeł przyczyn lecz opisuje objawy. Tak naprawdę jednak zmienność mierzy po prostu… zmienność. Do pomiaru ryzyka używa się jej z głównie z powodu prostoty użycia ponieważ w ten sposób można je matematycznie skalować, a liczbami da się prościej zarządzać niż nieokreślonością.
Jak wynotowałem z niedawno czytanej książki Jacka Schwagera “Market sense and nonsense”:
„Volatility is used as a proxy for risk because it is easily quantified, not because it is appropriate” („Zmienność jest używana jako zastępstwo dla ryzyka ponieważ jest łatwo wyliczalna, a nie dlatego, że jest to właściwe”).
Zdaje się jednak, że nie ma takiej siły, która owo tak powszechne użycie tej równości mogłoby zmienić. Co więcej – nie sposób przyjąć innej, pojedynczej miary, która byłaby w pełni odpowiednia, ryzyko przyjmuje bowiem wiele oblicz zależnie od postrzegania inwestora. Dla mnie może to być potencjalna możliwość straty w pojedynczej transakcji lub serii strat (drawdown) niezwiązane ze zmiennością, dla kogoś innego to po prostu nie osiągnięcie zakładanego zwrotu, a np. dla długoterminowego podejścia „kup i trzymaj” korekty cen budujące zmienność są w zasadzie nieistotne.
Na koniec jeszcze małe posłowie odnośnie funduszy inwestycyjnych. Kiedyś w dyskusjach przywołałem swoją rozmowę z jednym z zarządzających, którego dociskałem pytaniem dlaczego tak tę zmienność z ryzykiem utożsamiają. Powiedział mi, że zmienność (lub inaczej – gwałtowność zmian) jako miara ryzyka ma znaczenie głównie dla kupujących jednostki funduszy. Im wyższe bowiem wahania wycen tym większa szansa, że klienci funduszy przestraszą się tego wychodząc z inwestycji ze stratą (zresztą to samo może dotyczyć niedoświadczonych inwestorów indywidualnych na rynku akcji). To tworzy dodatkowe kaskady spadków wycen funduszu spowodowane koniecznością wyprzedaży przez niego aktywów w najmniej odpowiednim momencie. Dlatego też fundusze hedgingowe stosują tzw. ‚lock period’ czyli ustalają okresy czasu gdy kapitał nie może być wycofywany przez klientów.
O wpływie owych fluktuacji pisze we wspomnianej wyżej książce Schwager, który sam zarządza funduszem funduszy:
„The more downside volatility the greater the likelihood investors will exit on a drawdown even if fund always recovers to new highs”
(“Im więcej zmienności dolnoprzedziałowej tym większe prawdopodobieństwo tego, że inwestorzy wyjdą podczas obsunięcia kapitału, pomimo tego, że fundusz zawsze powraca do nowych szczytów”)
—kat—

20 Komentarzy
Dodaj komentarz
Niezależnie, DM BOŚ S.A. zwraca uwagę, że inwestowanie w instrumenty finansowe wiąże się z ryzykiem utraty części lub całości zainwestowanych środków. Podjęcie decyzji inwestycyjnej powinno nastąpić po pełnym zrozumieniu potencjalnych ryzyk i korzyści związanych z danym instrumentem finansowym oraz rodzajem transakcji. Indywidualna stopa zwrotu klienta nie jest tożsama z wynikiem inwestycyjnym danego instrumentu finansowego i jest uzależniona od dnia nabycia i sprzedaży konkretnego instrumentu finansowego oraz od poziomu pobranych opłat i poniesionych kosztów. Opodatkowanie dochodów z inwestycji zależy od indywidualnej sytuacji każdego klienta i może ulec zmianie w przyszłości. W przypadku gdy materiał zawiera wyniki osiągnięte w przeszłości, to nie należy ich traktować jako pewnego wskaźnika na przyszłość. W przypadku gdy materiał zawiera wzmiankę lub odniesienie do symulacji wyników osiągniętych w przeszłości, to nie należy ich traktować jako pewnego wskaźnika przyszłych wyników. Więcej informacji o instrumentach finansowych i ryzyku z nimi związanym znajduje się w serwisie bossa.pl w części MIFID: Materiały informacyjne MiFID -> Ogólny opis istoty instrumentów finansowych oraz ryzyka związanego z inwestowaniem w instrumenty finansowe.

Łezka się w oku kręci. Przypomina mi się, jak jeszcze w ubiegłym wieku na pewnej grupie usenetowej rozpisywałem się o tym, że zmienność jako miara ryzyka w teorii Markovitza jest bez sensu, a Ty wraz z kolegą Limakiem odsądzaliście mnie od czci i wiary, że niby szargam noblowe świętości i gadam głupoty. Ale to taka dygresja, oczywiście bez złośliwości. W sumie jako sama miara ryzyka zmienność jest mniej więcej tyle samo warta co inne pomysły, o dziwo sam intuicyjnie postrzegam rozchwiane rynki jako ryzykowne, natomiast użycie zmienności jako miary ryzyka w teorii portfeli optymalnych jest totalnym nieporozumieniem i bezsensem, oczywiście według mnie. Ale takie akademickie rozważania dawno już przestały mnie podniecać, trzeba panie pipsy liczyć i tyle…
@ kathay
Ja mam kilka ważnych (i mniej ważnych) pytań, w związku z tym tekstem, być może nawet w 10 częściach!
Pytanie 1: Co Markowitz opublikował w 1952 r?
Pytanie 2: W którym roku opublikowano Modern Portfolio Theory (moozna się pomylić o rok :))?
Pytanie 3 – Czy o tak zwanej semiwariancji kolega słyszał (i co o niej myśli jako o ewentualnej mierze ryzyka)?
cdn (niechybnie)
PS
Sugeruje poprawić tłumaczenie „downside volatility” gdyż „zmienność spadkowa” mnie razi a poza tym może wprowadzać w błąd.
‚Ale takie akademickie rozważania dawno już przestały mnie podniecać, trzeba panie pipsy liczyć i tyle…’
dokładnie TAK!! 🙂 brakuje nam tu praktyki, a teoretycznych rozważań jest bez liku i daje sobie uciąć pare zer na koncie , ze NIGDY się nie skończą..
ważne pytanie nr 100 : a jak tam u Panstwa z praktyką?
ale o tym sza.. to tabooooo..
Less, tak przy okazji. Jeżeli możesz przelej kilka kropli ze swej cysterny wiedzy, gdyż albowiem w tych sprawach jesteś dla mnie wyrocznią. Napisałem że trzeba pipsy liczyć, ale wszak pips to pluralis. Purystą nie jestem, ale sztuka cierpi. Należało napisać, że trzeba pipy liczyć, ale trochę nie najlepiej się to konotuje. Jak z tego wybrnąć?
@ nieudacznik
„Napisałem że trzeba pipsy liczyć, ale wszak pips to pluralis. Purystą nie jestem, ale sztuka cierpi. Należało napisać, że trzeba pipy liczyć, ale trochę nie najlepiej się to konotuje. Jak z tego wybrnąć?”
I dobrze napisałeś, bo pipst to są ziarenka w owocu (np. w jabcu nie mylić z jabcokiem) a jak mówi przysłowie – ziarko do ziarka zbierze się miarka.
A jak wybrnąć z tej konfuzji? Ano widzę dwa wyjścia, dalej tak trzymać, gdyż u nas, jakoś tak, przyjęło się mówić raczej pips niż pip (tak jak drzwi czyli pluralis).
A jak z tym się czujesz nieswojo to możesz mówić pieszczotliwie pipsiak, tylko uważaj by za te pipsiaki nie iść do paki.
PS
Dawniej to się mówiło że się zalicza a nie liczy, to co ci się trochę nie najlepiej konotuje, ale dziś nie tyle sztuka cierpi ile artysta! 🙂
Tylko z tym puryzmem uważaj, bo jak kumple przy oglądaniu meczu wyślą kogoś po piwo i chipy, to może się źle skończyć
@nieudacznik
Dyskusji nie pamiętam, ale chętnie bym ją przeczytał ponownie o ile jest gdzieś w archiwum, głównie po to by zobaczyć dlaczego upierałem się przy takiej interpretacji.
@less
Markowitz, H.M. (March 1952). „Portfolio Selection”. The Journal of Finance
http://www.math.ust.hk/~maykwok/courses/ma362/07F/markowitz_JF.pdf
O semiwariancji nie piszę ponieważ jest w przeciwieństwie do odchylenia standardowego rzadko używana, zresztą w praktyce rynek posługuje się samym terminem zmienność, w AT częściej okraszana literkami ATR.
Jak sugerujesz przetłumaczyć to „downside vol”? Chętnie to zrobię o ile uzgodnimy wersję
Co do praktyczności – musiałbym zrobić odrębny wpis.
Analizy są pełne nieprawidłowego użycia zwrotu rośnie vol= rośnie ryzyko, to tylko robi wodę z mózgu czytającym. A problem właściwego zrozumienia znaczenia ryzyka to osobna sprawa, którą obserwuję w mailach i rozmowach. Jeśli same fluktuacje stają się dla inwestora przerażającym doświadczeniem to wypada edukację zacząć od nowa.
@ kathay
No właśnie, w 1952 r. Markowitz opublikował ten artykuł (dysertacja doktorska), ale daleko jeszcze było do MPT. Można powiedzieć że była to koncepcja (zapłodnienie znaczy się) ale MPT jeszcze się nie narodziło, bo wykluwała się dużo dłużej niż słonica chodzi w ciąży.
Zasadniczo to dopiero to ten artykuł nie wzbudził zainteresowania przez wiele lat i dopiero po jego książce z 1959 r. – „Portfolio Selection: Efficient Diversification of Investments”, temat trochę ruszył, choć w międzyczasie swój wkład Roy (1952), Tobin (1958), a na początku lat 60-tych, Treynor, Sharpe, Fama a potem Ross.
Tak że MPT tak naprawdę narodziła się, poszła w świat, gdzies w połowie lat 60-tych.
Nie jest prawdą, że semiwariancja jest rzadko używana, rzadziej zapewne, ale wcale nie tak rzadko – stosuje się ja do oceny portfela (Sortino ratio), do minimalizacji hedge ratio, itp.
Zreszta o semiwariancji jako lepszej mierze pisał sam Markowitz (pierwszy był tu Roy) w 1959 roku, gdyż uważał że liczy się downside deviation (czyli zmiennośc poniżej wartości oczekiwanej) tak naprawdę, do oceny ryzyka.
Semiwariancja jako miara downside risk, z rodziny tzw lower partial moments (wprowadzonych dopiero w drugiej połowie lat 70-tych) jest dużo lepszą miarą więc profesjonaliści ją stosują.
„Jak sugerujesz przetłumaczyć to „downside vol”? Chętnie to zrobię o ile uzgodnimy wersję.”
Ja nic nie sugeruję od siebie, bo ktoś to już wcześniej zgrabnie określił jako „zmienność dolnoprzedziałową”, więc podejrzewam że tu nic lepszego nie wymyślę.
Określenie „zmienność spadkowa” wprowadza w błąd, gdyż sugeruje jakiś spadek(cen, stóp zwrotu itp.) natomiast tu chodzi o wyniki (dane wejściowe) poniżej średniej lub wartości zadanej (minimalny zwrot oczekiwany), które przecież mogą wystąpić również na wzroście.
cdn…
Dziękuję za tę notkę. Czytam w miarę regularnie Wasze blogi od jakichś trzech lat (oczywiście kocham Was za to) i zawsze omawiając kwestię ‚ryzyka a zmienności’ poprzestawano tutaj na sloganie ‚ryzyko nie jest tożsame ze zmiennością, o czym już pisaliśmy miliard razy’ i szczerze mówiąc nigdy tego znaleźć nie mogłem tutaj, i głupi się czułem, jednocześnie wstydząc się dopytywać, ale nareszcie wiem o co Wam chodzi 😉
Niestety wciąż we mnie więcej akademika niż praktyka, więc przynudzę Was kilkoma akapitami.
Przede wszystkim dość logiczne jest to co napisałeś, Kathayu, ale zastanawiam się jak to się ma do współczynnika zmienności (CV – Coeffitient of Variation). Wszak odchylenie standardowe jest miarą bezwzględną, a CV miarą relatywną, którą się liczy jako iloraz odchylenia standardowego i średniej arytmetycznej stóp zwrotu, a więc jeśli akcja cały czas jest zyskowna, tak jak na pierwszym schemaciku pomimo zygzaka, to jej CV będzie niższe. Uprzejmie proszę o ustosunkowanie się do tego.
Fajnie, że w komentarzach poruszono kwestię semiodchylenia standardowego. Elton&Gruber w swojej ksiązce H Jajuga gdzieś tam pisali, że liczenie semiwariancji mija się z celem, bo badania dowiodły, że w dół jest ona taka sama jak w górę, więc lepiej posługiwać się wariancją i odchyleniem standardowym. I tak się zastanawiam – czy faktycznie wciąż tak jest, że nie jest to kwestia warta badania (rozkład tych zmienności), czy też bezrefleksyjnie to łyknięto. Swoją drogą podręczniki zarówno Haugena jak i Elton&Gruber zwą się ‚nowoczesnymi’ teoriami portfelowymi i jak się spojrzy do ich bibliografii to można po prostu uklęknąć, bo te nowoczesne teorie się wykluwały z multum, multum papersów, tak jak lesserwisser to tutaj nam ładnie zakiełkował tę myślą.
Dobra, kwestia ryzyka u akademików. Róóóżnie je definiowano. Zdaniem J.C. Van Horna i J.M. Wachowicza Jr., ryzyko to rozbieżność pomiędzy osiągniętymi dochodami, a oczekiwanymi . A.C. Shapiro zdefiniował ryzyko jako dyspersje możliwych wyników wokół oczekiwanego zwrotu . A.J. Keown, D.F. Scott Jr, J.D. Martin, J.W. Pretty zdefiniowali ryzyko jako potencjalną zmienność przyszłych przepływów pieniężnych . „Im większy jest przedział tej zmienności, tym ryzyko jest większe”. Według G.J. Alexandra, W.F. Sharpe’a i J.V. Bailey’a ryzyko jest utożsamiane z niepewnością związaną z przyszłą wartością dokonywanych inwestycji . A teraz kwestia rozróżniania ryzyka i niepewności: taka A. Duliniec za ryzyko przyjęła, że to jest sytuacja, w której istnieje prawdopodobieństwo osiągnięcia wyników większych lub mniejszych od prognozowanych i znany jest rozkład prawdopodobieństwa i odchyleń tych wyników od ich wartości oczekiwanych – prawdopodobieństwo te daje się zmierzyć; natomiast niepewność to sytuacja gdzie rozkład prawdopodobieństwa rozbieżności wyników od ich wartości oczekiwanych nie jest znany i nie jest możliwy do oszacowania . „Ryzyko to dająca się zmierzyć niepewność” .
I jeszcze jedno. Przeczytałem w swoim życiu tony podręczników akademickich do finansów przedsiębiorstw i rynku, głównie amerykańskich, ale też polskich, cała klasykę praktycznie, i szczerze mówiąc ze wskaźnikiem Sortino spotkałem się dopiero podczas Computional Investing na coursera.org. Ze wskaźnikiem Modiglianich dopiero w broszurach jednego z domów maklerskich. Jak żyć?
A teraz offtop: @lesserwisser; czy mogę od Trystera wziąć maila do Ciebie i napisać do Ciebie dwa mocno niestandardowe pytania z rynku, z którymi mam mindfucki? Obiecuję, że nie są zbyt absorbujące…
@ Bebok
Trafne pytanie z tym współczynnikiem zmienności (cv)!
Zresztą inne kwestie poruszone są też warte pochylenia się. Nie bardzo rozumiem czemu kolega Tomasz już pogonił do części 11, bo temat jest ważny, ciekawy i potencjalnie pomocny.
W nagrodę wujek less da ci namiary na Sortino ratio i M2.
Co do Sortino ratio to podaje namiar na dobry poglądowy artykuł z Futures (luty 2013) – „Sortino ratio: A better measure of risk”, gdzie
ciekawe sa rysunki, które nie zaszkodzą również Kathayowi 🙂
(vide downside volatility).
Jeśli chodzi o podstawowe podręczniki to wskaźnik zwany M2
(M squared) opisany jest chyba tylko w „Investment” Bodie, Cane Marcus (str 823-24 wyd. z 2010 r.), jest na pewno w wyd 6 z 2005 r. i o ile się nie mylę również w wyd 5. z 2001 r.)
Namiar na oryginalny artykuł Franco i Leah Modigliani – Risk adjusted performance, jest poniżej.
http://bbs.cenet.org.cn/uploadImages/20035715461865606.pdf
Jeśli chodzi o pytania mózgotrzepy to chętnie pomogę (o ile będę w stanie) – jeśli możesz podać swój mail to się z Tobą skontaktuję, a jak wolisz nie podawać to mogę przejść przez bossa.
Generalnie sugeruję zamieszczenie pytań na stronie blogu bo inni tez mogą się przyczynić a mogą też być pomocne innym.
@ Bebok
http://www.futuresmag.com/2013/02/01/sortino-ratio-a-better-measure-of-risk
@ Bebok
Sprawdziłem tego Jajugę, bo mnie to nurtowało, coś ci się pokićkało bo on dobrze pisze, choć mógłby to wyrazić bardziej przejrzyście:
„Zauważmy, że w powyższym przykładzie semiwariancja równa się połowie wariancji. Zdarza się tak zawsze wtedy, gdy rozkład stopy zwrotu jest symetryczny. Jeśli rozkład nie jest symetryczny, to wiadomo jedynie, że semiwariancja jest mniejsza od wariancji.”
Tu nie jest trafione słowo „zawsze” bo wystarczy samo „wtedy”, już lepsze by było ujęcie „jedynie wtedy”.
Gdy rozkład jest symetryczny (mediana i moda równają się średniej) to semiwariancje (dolna i górna) są równe a wariancja jest oczywiście SemiVr.
Gdy rozkład jest asymetryczny to semiwariancje górno i dolno -przedziałowe są różne. Przy skośności prawostronnej semiwariancja górna jest większa, a przy skośności lewostronnej (tej złej) to oczywiście semiwariancja dolna na jest większa.
eee…
„Gdy rozkład jest symetryczny (mediana i moda równają się średniej) to semiwariancje (dolna i górna) są równe a wariancja jest oczywiście równa 2 SemiVar.”
@less: dzięki 🙂 Ej, nie powiedziałem że jak Jajuga to z „Inwestycje” (bo stamtąd wziąłeś cytat), ale pewnie masz rację, coś koślawo zapamiętałem jego słowa.
Mam nadzieje, że Kath jakoś się odniesie do współczynnika 😛
@less
Zmieniłem tę zmienność w tekście specjalnie dla ciebie 🙂 Choć myślę, że dla zrozumienia przez większość czytających łatwiej byłoby zrobić rysunek. Ryzyko to spory abstrakt dla wielu inwestorów, tak to odbieram po wielu rozmowach.
Jestem przez ostatnie tygodnie w mocnym niedoczasie więc dla nie to luksus przeczytać wszystkie komentarze i odpowiedzieć. Zawsze jeśli coś pominę to śmiało piszcie na kathay w bossa kropka pl, z pewnością wrócę do wpisu i odpiszę w wolnym czasie
@Bebok
Co do ryzyka i niepewności trafnie wnioskujesz. Najprościej różnicę wyjaśnia właśnie możliwość parametryzacji.
Co do CV:
skoro wg. tego wskaźnika wykres lewy jest mniej zmienny to odwróćmy nieco kierunki i załóżmy, że krzywa po lewej schodzi coraz niżej, a po prawej coraz wyżej z taką samą gwałtownością. Skoro niższa zmienność jest wyznacznikiem to wówczas inwestycja z lewej byłaby bezpieczniejsza. Kręcimy się w kółko.
Poza tym na określenie zmienności używa się w literaturze wariancję lub odchylenie standardowe. Spróbuj pokombinować dlaczego nie CV?
@less
Jak widzisz oblatany w teorii Bebok pisze, że nie wiedział o Sortino (a ja kiedyś zrobiłem wpis tutaj o tym lata temu chyba). Masz dowód na to jak często się tego używa. Z tego co sam obserwuje Sortino czasem stosuje się do oceny funduszy, ale nie do pomiaru ryzyka rynku.
Mój stosunek do tych miar jest ambiwalentny. Sam nie stosuję zmienności w charakterze ryzyka, ale powtórzę, że nic mi do tego jeśli komuś pozwala to zrozumieć, ocenić i ograć rynek.
@kathay: Dziękuję za odniesienie się do mojego teoretycznego wywodu 😉
Zależy co masz na myśli pisząc o tym, że nie używa się CV – to że nie mówi się o nim w ogóle, czy to że się o nim mówi, ale potem w dalszych wywodach i tak się ogranicza kwestię zmienności do wariancji i odchylenia standardowe. Jeśli to drugie to masz rację, jeśli to pierwsze, to w wieeelu pozycjach widziałem opis CV. Przy opisie CV częstokroć zwraca się uwagę na to, że jest on przydatny wtedy, i tylko wtedy, gdy jego wartość jest dodatnia(!). Gdy jest ujemna jego interpretacja mija się z celem(!). Czy to miałeś na myśli, żebym wykombinował czy coś innego? 🙂