Dotarły dziś do mnie informacje o badaniach, które przeprowadził Pablo Pena z Uniwersytetu w Chicago, a których celem było sprawdzenie czy dni urodzin tworzą jakąś anomalię w śmiertelności Amerykanów. Badanie spotkało się z zainteresowaniem mediów, którego wyrazem jest choćby artykuł w Washington Post.
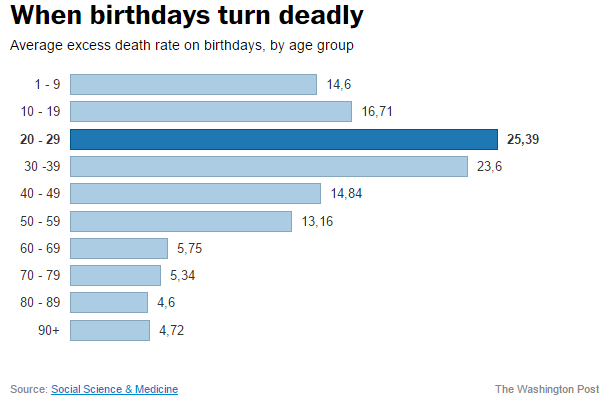
Według dziennikarza Washington Post, Pena przeanalizował dane o śmierci około 25 milionów Amerykanów w latach 1998-2011 i po uwzględnieniu sezonowych trendów w śmiertelności sprawdził czy w dniu swoich urodzin Amerykanie borykają się z wyższym ryzykiem śmierci. Okazało się, że tak właśnie jest. Przeciętnie, w dniu urodzin ryzyko śmierci jest o 6,7% wyższe niż w każdym innym dniu. W przypadku młodych ludzi (w wieku 20-29) ryzyko to rośnie o około 25%. Urodziny przypadające w weekend wiążą się z dodatkowym ryzykiem. Poniższa tabela podsumowuje wyniki:
Wyniki, które uzyskał Pena dosyć dobrze komponują się z hipotezą tragicznych konsekwencji hucznych obchodów urodzin. Nie jest więc zaskoczeniem, że media zainteresowały się badaniami, które najczęściej przedstawiały tak jak artykuł w Washington Post, zatytułowany: Masz większe ryzyko umrzeć w dniu swoich urodzin.
Naturalnie, nie zamierzam zajmować się samym problem śmiertelności i wpływu na nią urodzinowych imprez. Sposób w jaki wyniki badań zostały przedstawione w mediach uważam jednak ze dobry pretekst do przypomnienia, że nie wszystkie pojawiające się w mediach dane statystyczne mają znaczenie.
Proszę zwrócić uwagę, że wszystkie podane niżej obliczenia mają charakter wykonanych na serwetce i ich celem nie jest polemika z badaniami Pablo Peny. Moim zamierzeniem jest pokazanie, że czasem szczypta intelektualnej ciekawości wystarczy by poznać rzeczywistą wartość rozpowszechnianych w mediach informacji statystycznych.
Załóżmy, że jesteśmy w najbardziej narażonej na efekt urodzin grupie wiekowej. Czy 25% wzrost ryzyka śmierci powinien zrobić na nas wrażenie? Roczne prawdopodobieństwo śmierci w tym przedziale wiekowym to około 1100 do 1. Z 1100 dwudziestokilkulatków każdego roku umiera jeden pechowiec. Jeśli pominiemy sezonowość śmiertelności to uzyskamy przeciętne dzienne prawdopodobieństwo śmierci na poziomie około 1 do 400 000. W dniu urodzin wzrośnie ono do 1 do 320 000. Tak więc ten 25% wzrost ryzyka śmierci, to wzrost z 0,00025 do 0,00031. Takie przedstawienie problemu nie przyciąga jednak uwagi tak bardzo jak wzrost o 25%.
Ten minimalny wzrost ryzyka śmierci przekłada się jednak na całą populację. Być może w tym kontekście przybiera znaczące rozmiary i na przykład sugeruje przeprowadzenie jakiejś akcji społecznej. Jeśli weźmiemy pod uwagę populację dwudziestokilkulatków w USA to cały efekt urodzin tworzy rocznie mniej niż 30 dodatkowych zgonów w tej grupie wiekowej. Czy to jest liczba wskazująca na istnienie poważnego problemu, któremu należy jakość spróbować przeciwdziałać? Nie wiem.
Mam nadzieję, że ten prosty przykład skłoni czytelników do sceptycznego podchodzenia do przekazywanych w mediach danych statystycznych, także tych dotyczących rynków finansowych (na przykład wyników spółek). W sytuacji, w której celem osoby przedstawiającej te dane jest przyciągnięcie naszej uwagi a nie przekazanie nam jak najbardziej pożytecznej informacji, bezrefleksyjne chłonięcie przekazywanych informacji nie poprawia ani rzeczywistej wiedzy o świecie ani procesu decyjnego.

4 Komentarzy
Dodaj komentarz
Niezależnie, DM BOŚ S.A. zwraca uwagę, że inwestowanie w instrumenty finansowe wiąże się z ryzykiem utraty części lub całości zainwestowanych środków. Podjęcie decyzji inwestycyjnej powinno nastąpić po pełnym zrozumieniu potencjalnych ryzyk i korzyści związanych z danym instrumentem finansowym oraz rodzajem transakcji. Indywidualna stopa zwrotu klienta nie jest tożsama z wynikiem inwestycyjnym danego instrumentu finansowego i jest uzależniona od dnia nabycia i sprzedaży konkretnego instrumentu finansowego oraz od poziomu pobranych opłat i poniesionych kosztów. Opodatkowanie dochodów z inwestycji zależy od indywidualnej sytuacji każdego klienta i może ulec zmianie w przyszłości. W przypadku gdy materiał zawiera wyniki osiągnięte w przeszłości, to nie należy ich traktować jako pewnego wskaźnika na przyszłość. W przypadku gdy materiał zawiera wzmiankę lub odniesienie do symulacji wyników osiągniętych w przeszłości, to nie należy ich traktować jako pewnego wskaźnika przyszłych wyników. Więcej informacji o instrumentach finansowych i ryzyku z nimi związanym znajduje się w serwisie bossa.pl w części MIFID: Materiały informacyjne MiFID -> Ogólny opis istoty instrumentów finansowych oraz ryzyka związanego z inwestowaniem w instrumenty finansowe.

Jednym ze szczególnych przykładów statystycznej bezmyślności i braku odpowiedniej wiedzy są m.in. przekazy lekarzy oraz kampanie przeróżnych fundacji i innych organizacji „troszczących się” o zdrowie populacji dotyczące badań przesiewowych w kierunku wykrywania nowotworów np. raka piersi lub prostaty. W konsekwencji błędny przekaz statystyczny prowadzi często do błędnych i szkodliwych wyborów podejmowanych przez ludzi.
http://time.com/author/gerd-gigerenzer/
Mam wrazenie, ze ten rodzaj „danych” dominuje w przekazie finansowym. Wszelkie ekscytacje, ze zysk wzrósł z 5,02 na 5,03 na akcje; że zbiory pszenicy wzrosły o 100 000 buszli, bez podania całości itp itd.
Albo w przeszłości „na prawach poboru XYZ mozna bylo zarobic 1000%” NIc, to ze obrot był 10 złotych.
Lubimy duże szokujace liczby i nie próbujemy sie zastanawiac nad całością
Odpowiedzia ludzi na dane nie są one same tylko ich percepcja.
Stąd popularne powiedzenie „dobry bajer nigdy nie jest zły” 🙂
Przy okazji rozmowy o procentach, warto przypomnieć/zwrócić uwagę na to, że wyniki indeksów giełdowych podawane w procentach są bardzo zwodnicze i spadek o iles procent nie równa się wzrostowi o tyle samo procent. Np. 260+50%=390, ale w drugą stronę: 390-50%=195.
Analogicznie: 260-50%=130, ale żeby odrobić tę stratę kurs musiałby wzrosnąć jednorazowo o 100% albo wzrosnąć kilka razy (np. 130+50%=195+34%=260,3)