Znalazłem niedawno interesujące dane, które dobrze ilustrują zalety regularnego inwestowania w długim horyzoncie czasowym.
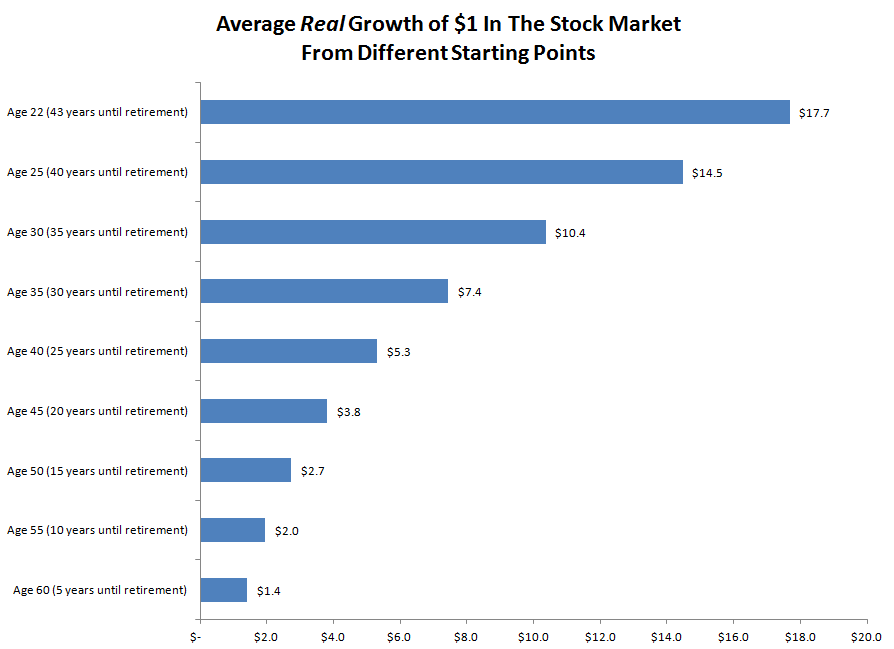
Na stronie Millennial Invest opublikowano zestawienia zysków z inwestycji na amerykańskim rynku finansowym (w akcje, obligacje i bony) w różnych horyzontach czasowych – w zależności od tego czy ktoś zaczyna inwestowanie w wieku 22, 30, 40 czy 50 lat. Poniższy wykres pokazuje co działo się z zainwestowanym dolarem na amerykańskim rynku akcyjnym w różnych horyzontach czasowych przy założeniu przeciętnej rocznej realnej stopy zwrotu (6,9%) w okresie od 1926 roku (do 2014 roku):
Przy analizie tego wykresu warto pamiętać o dwóch faktach: oparty jest o dane z najprawdopodobniej bardzo szczęśliwego rynku akcyjnego, z najprawdopodobniej bardzo udanego okresu. Choć jestem umiarkowanym optymistą to wydaje się mi, że oczekiwanie w najbliższych dekadach realnych stóp zwrotu na tym poziomie może być wyrazem nadmiernego optymizmu.
Tym niemniej, wykres dobrze pokazuje korzyści z przyjęcia długiego horyzontu czasowego w największym dla większości ludzi projekcie inwestycyjnym czyli oszczędzaniu na własną emeryturę. W trzeciej dekadzie życia większość ludzi stoi nie tylko przed wyborem oszczędzanie czy konsumpcja ale także przed dużo trudniejszym wyborem oszczędzanie czy inwestycja w siebie (zapewniająca potencjalnie wyższe dochody w przyszłości). Powyższe zestawienie może zachęcić do decyzji o rozpoczęciu, chociaż w niewielkim wymiarze finansowym, emerytalnego programu inwestycyjnego tak wcześnie jak to możliwe.
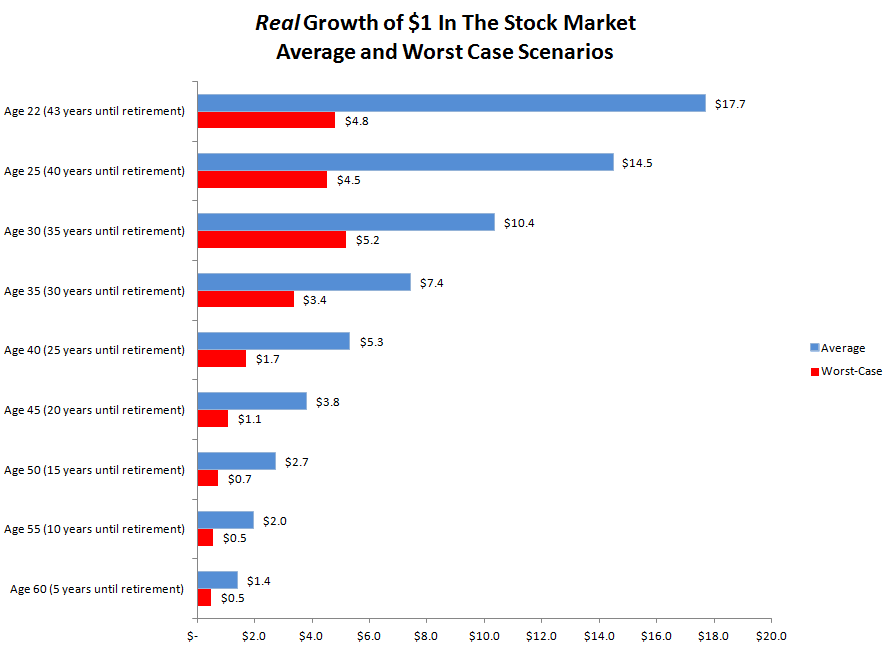
Przyjęcie długiego terminu w oszczędzaniu na emeryturę ma jeszcze jedną zaletę, którą można nazwać dywersyfikacją czasową. Zalety dywersyfikacji czasowej czyli rozłożenia inwestowania na wiele lat pokazuje poniższy wykres, na którym zamieszczono wyniki inwestycji na amerykańskim rynku akcyjnym w przeciętnym scenariuszu i najgorszym możliwym scenariuszu. Okres od 1926 roku obejmował kilka niezbyt udanych okresów na rynku akcyjnym z Wielkim Kryzysem i straconą dekadą na przełomie lat 60. i 70. na czele.
Jak widać, nawet na bardzo szczęśliwym rynku akcyjnym, w bardzo udanym okresie zdarzały się kilku, kilkunastoletnie okresy bardzo słabych stóp zwrotu i negatywnych stóp zwrotu. W przypadku najgorszego scenariusza różnice w rocznych stopach zwrotu w różnych okresach czasowych są spore: od 3,8% w 43-letnim horyzoncie czasowym, przez 0,5% w 20-letnim horyzoncie czasowym do -7% i -16% w odpowiednio 10-letnim i 5-letnim horyzoncie.
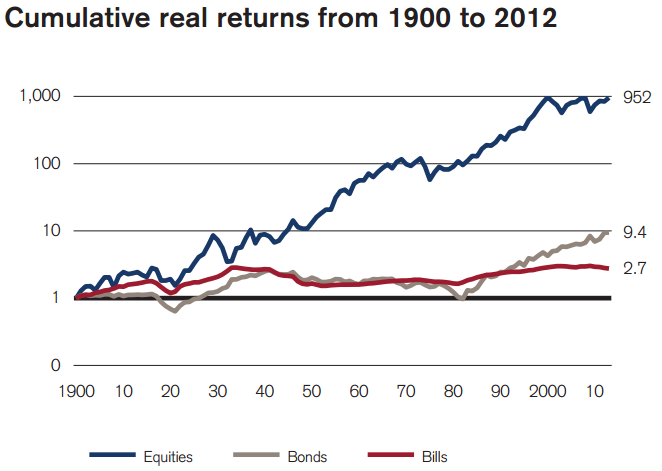
Co ciekawe, z zestawień wynika, że na rynkach obligacji i bonów zdarzały się dużo dłuższe okresy słabych stóp zwrotu. Szczerze mówiąc, musiałem sprawdzić czy pokazane dane są poprawne bo 40-letnie okresy na rynku obligacji i bonów, które przyniosły inwestorom odpowiednio 70% i 40% skumulowanych strat wydały się podejrzane. Dane są poprawne, zgadzający się z tymi z Credit Suisse Global Investment Returns Yearbook:
Jeśli więc założymy, że struktura rynku nie ulegnie gwałtownym zmianom w najbliższych dekadach to okaże się, że istnieją sensowne przesłanki by rozpocząć emerytalny projekt inwestycyjny w jak najwcześniejszym okresie życia.

9 Komentarzy
Dodaj komentarz
Niezależnie, DM BOŚ S.A. zwraca uwagę, że inwestowanie w instrumenty finansowe wiąże się z ryzykiem utraty części lub całości zainwestowanych środków. Podjęcie decyzji inwestycyjnej powinno nastąpić po pełnym zrozumieniu potencjalnych ryzyk i korzyści związanych z danym instrumentem finansowym oraz rodzajem transakcji. Indywidualna stopa zwrotu klienta nie jest tożsama z wynikiem inwestycyjnym danego instrumentu finansowego i jest uzależniona od dnia nabycia i sprzedaży konkretnego instrumentu finansowego oraz od poziomu pobranych opłat i poniesionych kosztów. Opodatkowanie dochodów z inwestycji zależy od indywidualnej sytuacji każdego klienta i może ulec zmianie w przyszłości. W przypadku gdy materiał zawiera wyniki osiągnięte w przeszłości, to nie należy ich traktować jako pewnego wskaźnika na przyszłość. W przypadku gdy materiał zawiera wzmiankę lub odniesienie do symulacji wyników osiągniętych w przeszłości, to nie należy ich traktować jako pewnego wskaźnika przyszłych wyników. Więcej informacji o instrumentach finansowych i ryzyku z nimi związanym znajduje się w serwisie bossa.pl w części MIFID: Materiały informacyjne MiFID -> Ogólny opis istoty instrumentów finansowych oraz ryzyka związanego z inwestowaniem w instrumenty finansowe.

Warto ten wykres pokazać obok depozytów i %5 składanych rocznie przez X lat. Wychodzi to około 8$, 7$, 5.5$, 4.3$, 3.4$ itd. Czyli pi razy drzwi w środku obu wykresów i ZAWSZE więcej od worst case.
No chyba że odpowiedzią na Twój ostatni wykres jest to że w akcjach uwzględnili inflacje, w bondsach już nie.
@ Radek
Wszystkie serie w ostatnim wykresie są realne czyli po uwzględnieniu inflacji.
Mógłbyś trochę więcej napisać o tych danych o depozytach bo nie do końca rozumiem, do jakich okresów odnoszą się te wartości końcowe inwestycji, które podałeś.
Od góry, czyli 1.05^43=8$, 1.05^40=7 itd. Adresowałem pierwsze dwa wykresy z posta. Jak rozumiem one nie uwzględniają (w odróżnieniu do ostatniego) inflacji?
Problem z tymi symulacjami jest taki, że mierzą stopy zwrotu rynku a nie inwestora.
Należy sobie zadać pytanie jak wygląda przebieg naszej inwestycji? Czy inwestujemy cały kapitał na samym początku (w wieku 22 lat) by wypłacić w wieku 60 lat, co sugeruje większość symulacji czy może jednak jest to rozłożone w czasie? To zdaje się pytanie retoryczne.
Ten jeden dolar wpłacony 40 lat temu jest tylko jednym z wielu dolarów wpłacanych w tym okresie. Średnia stopa zwrotu o niczym nie informuje bo stopy zwrotu z lat późniejszych mają większą wagę niż stopy zwrotu z lat wcześniejszych (z uwagi na wielkość wpłaconego kapitału kapitału). CAGR także nie ma tu zastosowania bo nie bierze pod uwagę faktu, że tylko niewielka część kapitału (ten wspomniany dolar) pracuje przez cały czas inwestycji.
Ten sam problem był widoczny w czasie debaty o stopie zwrotu ofe.
Wg mnie bardziej pożyteczną symulacją byłaby inwestycja 1$ co miesiąc lub rok (kwota inwestycji może być też skorygowana o inflację) a następnie obliczenie stopy zwrotu poprzez IRR.
Żeby zobrazować problem zróbcie w excelu symulację lokaty na 10% wpłacanej rocznie przez dziesięć lat i porównajcie średnią stopę vs cagr vs IRR
@ zagrodny
Te zestawienia nie mierzą stóp zwrotu (one pochodzą z historycznych danych z rynku amerykańskiego) tylko całkowity wynik inwestycji ten samej kwoty dla różnych horyzontów czasowych.
Rozumiem Twoją uwagę, że pod koniec inwestowania oszczędzający ma na rynku dużo więcej pieniędzy niż na początku i stan rynku pod koniec okresu inwestowania ma istotne znaczenie. Ten sposób myślenia odpowiada zresztą za popularną zasadę oszczędzania emerytalnego, która postuluje „obniżanie ryzyka” (cokolwiek miałoby to znaczyć, praktycznie znaczy niedoważanie akcji i przeważanie tzw. bezpiecznych aktywów – obligacji, bonów, gotówki) wraz ze zbliżaniem się do emerytury.
Natomiast to nie zmienia roli długiego okresu i procentu składanego w tworzeniu kapitału emerytalnego.
Chyba, że chciałeś zrobić takie samo zestawienie całkowitych wyników inwestycji ale z uwzględnieniem kolejnych stałych wpłat. Ale wtedy też byłaby konieczność użycia historycznych danych o stopach zwrotu rynku akcyjnego.
Nie neguję tezy o długim okresie i procencie składanym, mam jedynie uwagi metodologiczne.
1. Symulacja powinna obejmować kapitał rozłożony w czasie, żeby bardziej to przypominało realną sytuację inwestora a nie abstrakcję.
2. Metoda obliczania stopy zwrotu (i kapitału końcowego). Nie wiem skąd pochodzi te 6,9%. Czy to jest średnia z rocznych stóp zwrotu, średnia arytmetyczna, geometryczna, czy coś jeszcze innego. Wg mnie w tym przypadku najbliższe realnej sytuacji byłoby obliczenie kapitału końcowego poprzez uśrednienie wszystkich okresów (43 lat, 40, 35…itd.), przesuwając punkt startu co rok od 1926. Podnoszenie jednej wartości do n-tej potęgi to finansowa alchemia.
@ zagrodny
To jest przeciętna, realna, roczna stopa zwrotu z amerykańskiego rynku akcyjnego od 1926 do 2014.
Wg mnie w tym przypadku najbliższe realnej sytuacji byłoby obliczenie kapitału końcowego poprzez uśrednienie wszystkich okresów (43 lat, 40, 35…itd.), przesuwając punkt startu co rok od 1926.
Zgadzam się. Ba, myślę, że to jest wykonalne w Excelu. Gdy będę miał trochę wolnego czasu w jakiś weekend to nad tym pomyślę.
Ok, ale nie rozumiem co dokładnie znaczy „przeciętna”. Nie jest to wyjaśnione w linkowanym artykule i nie jest podane skąd pochodzi ta wartość.
@ zagrodny
To jest uwzględniający inflację CAGR dla indeksu SP500 w latach 1926-2014. Uwzględnia dywidendy. Pochodzi z danych historycznych z indeksu SP500. Możesz to sobie policzyć choćby z bazy Shillera bo zawiera dywidendy.
Zrobiłem sobie zestawienie w Excelu dla 43 letniego okresu i 5 letniego okresu. Przy założeniu, że oszczędza się 1 dolara (tylko w I scenariuszu co roku wpłaca się 1/43 dolara co roku, w II 1/5 dolara co roku) dla rzeczywistych danych z lat 1926-2014.
Różnice są oczywiście dużo mniejsze niż w powyższych zestawieniach ale ciągle pokazują siłę długiego terminu.