Dlaczego ludzie płacą za bezużyteczne prognozy?

W poprzednim tekście zwróciłem uwagę na eksperyment, w którym czwórka badaczy pokazała, że część ludzi (82% uczestników eksperymentu) gotowych jest płacić za iluzoryczne umiejętności prognozowania całkowicie losowych wydarzeń, takich jak rzut monetą.

Traktowałem omówienie badań Bou, Brandts, Cayon i Guillen jako wprowadzenie do eksperymentów przeprowadzonych przez Powdthavee i Riyanto w 2012 roku, których podsumowaniem jest artykuł Czy zapłaciłbyś za ewidentnie bezużyteczne porady? Test granic przekonań o bezsensie prognozowania.

Kluczowym motywem eksperymentów Powdthavee i Riyanto jest rzut monetą i gotowość do płacenia za prognozy rzutu monetą. To cecha wspólna obydwu badań. Różni je natomiast sama konstrukcja eksperymentów.

Powdthavee i Riyanto przeprowadzili swoje badania wśród studentów trzech uniwersytetów – dwóch z Tajlandii i jednego z Singapuru. Łącznie w badaniach (w 12 sesjach) uczestniczyło 378 studentów z różnych kierunków – humanistycznych, biznesowych, ścisłych i inżynieryjnych. Tak więc część uczestników badania miała za sobą zajęcia ze statystyki.

Badacze dołożyli wielu starań by przekonać uczestników badania, że rzuty monetą są uczciwe. Używano monet uczestników, które zmieniano po 2 i 4 rundzie (łącznie było 5 rund) a monetami rzucali wytypowani uczestnicy badania, których zmieniano co rundę.

Uczestnicy badania otrzymali kapitał początkowy (100 żetonów w Tajlandii i 300 w Singapurze). Niestety, wartość żetonów była niewielka (50 żetonów to około 1 dolar) – tak więc stawki w eksperymencie były bardzo niskie. Uczestnicy badania obstawiali kolejne rzuty monetą i wygrywali dwukrotność postawionych żetonów za poprawne odgadnięcie (nic nie wygrywali w przypadku pomyłki). Po wszystkich 5 rundach zatrzymywali swoje wygrane.

Każdy z uczestników otrzymał też na początku badania 5 zamkniętych kopert. Znajdowały się w nich prognozy rzutów monetą, które dopiero miały się odbyć. Uczestnicy mogli za 10 żetonów otworzyć kopertę przed rzutem monetą i zobaczyć prognozę. Ci, którzy nie zdecydowali się płacić za prognozę po każdej rundzie mieli otworzyć kopertę i sprawdzić czy prognoza była trafna czy błędna.

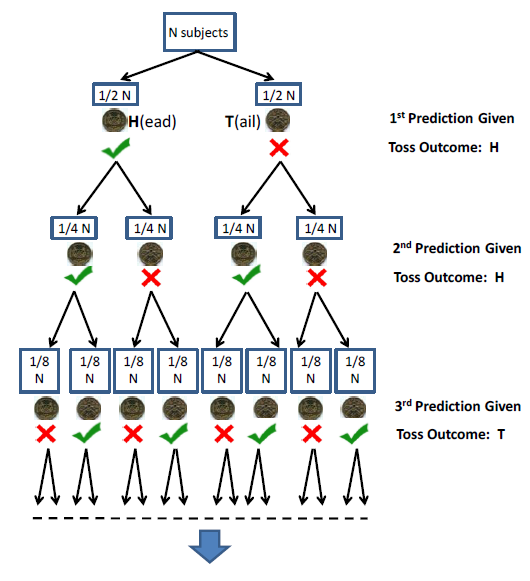
W tym miejscu autorzy badań zastosowali prosty lecz błyskotliwy trik – prognozy w kopertach ułożyli w drzewko by zagwarantować, że część uczestników badania będzie mieć do czynienia z serią poprawnych prognoz. To trik często stosowany przez iluzjonistów albo nieuczciwych ekspertów rynkowych. Połowie subskrybentów wysyła się jakąś prognozę a połowie prognozę przeciwną, następnie połowie z tych, którzy otrzymali poprawną prognozę wysyła się jakąś prognozę a połowie prognozę przeciwną – w ten sposób po kilku rundach część subskrybentów będzie przekonana, że czyta idealnie sprawdzające się prognozy. Poniższy rysunek przedstawia to graficznie:

Za Powdthavee i Riyanto

Dzięki temu trikowi na 378 uczestników badania:

• 191 otrzymało poprawną prognozę w pierwszej rundzie
• 92 w pierwszych dwóch rundach
• 48 w pierwszych 3 rundach
• 23 w pierwszych czterech rundach

W tym miejscu można już się domyśleć jednej z najważniejszych idei badania – naukowcy chcieli sprawdzić jak długa musi być seria poprawnych prognoz całkowicie losowego wydarzenia by przekonać ludzi, że warto zapłacić za te prognozy.

Zanim poznamy wyniki eksperymentu Powdthavee i Riyanto warto wrócić do dwóch błędów poznawczych, które mają duży wpływ na percepcję prawdopodobieństwa. Są nimi paradoks hazardzisty i efekt gorącej ręki. Choć można uznać te dwie postawy za wykluczające się wzajemnie to badania empiryczne pokazują, że współegzystują z sobą w dziedzinach, w których ludzie spotykają się z całkowicie losowymi lub w dużym stopniu losowymi wydarzeniami.

Paradoks hazardzisty to w uproszczeniu przekonanie, że istnieją większe szanse na przełamanie serii niż jej kontynuację. Po zaobserwowaniu 5 kolejnych wyrzuconych reszek ludzie mają skłonność obstawiać wyrzucenie orła w kolejnej rundzie. Paradoks hazardzisty zaobserwowano w rzeczywistych danych opisujących zachowanie graczy w ruletkę, graczy obstawiających psie i konne gonitwy oraz uczestników gier liczbowych.

Efekt gorącej ręki to z kolei przekonanie, że istnieją większe szanse na kontynuowanie serii niż jej przełamanie. Jørgensen, Suetens i Tyran pokazali występowanie tych dwóch błędów poznawczych w oparciu o rzeczywiste dane o decyzjach duńskich graczy w Lotto. Generalnie, większość graczy nigdy nie zmienia swojego zestawu liczb. Jeśli jednak zmieniają to dają się zauważać dwie anomalie – tuż po wylosowaniu danej liczby gracze mniej chętnie ją obstawiają ale efekt ten odwraca się gdy jakaś liczba losowana jest kilka razy pod rząd, a więc generuje serię.

Powdthavee i Riyanto sugerują, że w dużym uproszczeniu można założyć dominację paradoksu hazardzisty tam gdzie uczestnicy są mocno przekonani o losowym charakterze zjawiska generującego dane. Natomiast efekt gorącej ręki pojawia się z reguły wtedy gdy ludzie wnioskują, także błędnie wnioskują, że ludzkie umiejętności odgrywają rolę w generowaniu danej serii.

Tak więc konstrukcja badania Powdthavee i Riyanto umożliwiała obserwację tego jak wiele, a raczej jak niewiele, ludzie potrzebują by wyrobić sobie przekonanie, że ludzkie umiejętności odgrywały rolę w generowaniu serii. Przy tym cały czas warto pamiętać, że badanie dotyczyło rzutu monetą a więc zjawiska, o którym większość ludzi zdaje sobie sprawę, że jest całkowicie losowe. Eksperyment pokazuje więc jak niepozorny może być rozmiar udanej serii trafień by sprawić, że ludzie zapominają o całkowicie losowym charakterze procesu i zaczynają wierzyć w gorącą rękę.

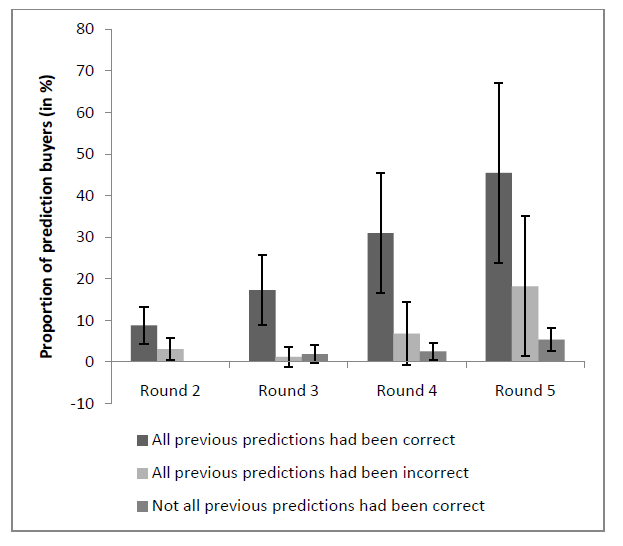
Poniższy rysunek pokazuję odsetek uczestników badania Powdthavee i Riyanto, którzy kupili prognozę w kopercie w kolejnych rundach dla trzech scenariuszy:

• wszystkie prognozy z kopert okazały się do tej rundy trafne
• wszystkie prognozy z kopert okazały się do tej rundy błędne
• prognoz z kopert były raz błędne raz trafne

Za Powdthavee i Riyanto

Jak widać, odsetek uczestników, którzy kupowali prognozę wzrósł z 9% dla pojedynczego trafienia prognozy do 43% dla serii czterech kolejnych trafień. Warto zauważyć, że w przypadku uczestników, którzy otrzymali w kopertach zmienne prognozy (raz trafne, raz błędne) odsetek kupujących wynosił od 1% do 4%.  Co więcej, badacze zauważyli, że uczestnicy eksperymentu, którzy kupili prognozy angażowali w zakłady w 3 ostatnich rundach zdecydowanie wyższe kwoty od uczestników, którzy nie kupili prognoz co sugeruje, że poważnie traktowali treść tych prognoz i wykazywali wiarę w ich pożyteczność.

Proszę zwrócić uwagę, że to wyniki po wykluczeniu 55 uczestników (14%), którzy kupili prognozy już przed I rundą co zdaniem badaczy mogło sugerować, że nie wierzyło w losowość rzutu monetą albo uczciwość rzutów monetą w eksperymencie.

Powdthavee i Riyanto nie zauważyli istotnych różnicy w skłonności do kupowania prognoz pomiędzy Tajlandczykami a Singapurczykami, kobietami i mężczyznami. Mierzony testem poziom wiedzy statystycznej był negatywnie skorelowany ze skłonnością do kupowania prognoz ale efekt ten był niewielki. Silnie negatywny efekt na skłonność do kupowania prognoz miało doświadczenie kupienia prognozy, która okazała się błędna w poprzedniej rundzie. Autorzy badań pozwolili więc sobie na stwierdzenie, że nie zaobserwowali statystycznie istotnych cech ludzi, które zwiększałyby ich skłonność do kupowania prognoz rzutów monetą.

Eksperymenty Powdthavee i Riyanto sugerują więc, że bardzo niewiele potrzeba by przekonać ludzi, że umiejętności mogą odgrywać istotną rolę w poprawnym prognozowaniu losowych zdarzeń. Wystarczająca może się okazać seria kilku poprawnych prognoz i to nawet wtedy gdy ludzie mają mocne powody by przypuszczać, że proces jest całkowicie losowy.

Wydaje się, że przypadku procesu, co do którego losowości ludzie nie są mocno przekonani (nie mają mocnego a priori) efekt gorącej ręki może być jeszcze silniejszy. To zagadnienie poruszę w następnym wpisie.