Jednym z problemów, z którym mierzą się analitycy techniczni jest wybór skali na wykresie. Czy korzystać ze skali liniowej (arytmetycznej), w której odległość między jednostkami cenowymi jest równa, czy też ze skali logarytmicznej, na której odległości odpowiadają procentowym zmianom. Dla tych, którzy monitorują rynki walutowe, na których procentowe zmiany (zwłaszcza w relatywnie krótkich okresach) nie są znaczące wybór skali nie będzie miał wielkiego znaczenia. Ale już na rynkach, gdzie zmiana nominalna wynosi kilkaset jednostek, a my chcemy zrobić analizę z jakiegoś dłuższego okresu, może być to niesłychanie paląca kwestia.
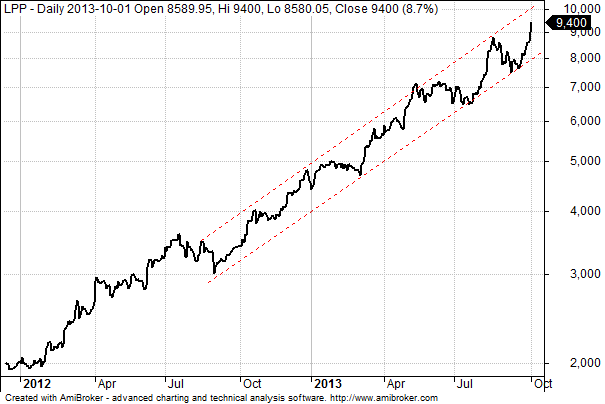
Spójrzmy na wykres najdroższych nominalnie akcji na GPW, czyli LPP.
Na początek wykres w skali logarytmicznej:
Bardzo zgrabnie wyrysowany kanał trendu, wyznaczający bieżący kierunek i mogący być nawet ostrzeżeniem (lub okazją) dla części graczy przez zbliżającą się silniejszą korektą na poziomie około 10 000 złotych, czyli po dojściu do górnego ograniczenia tego kanału.
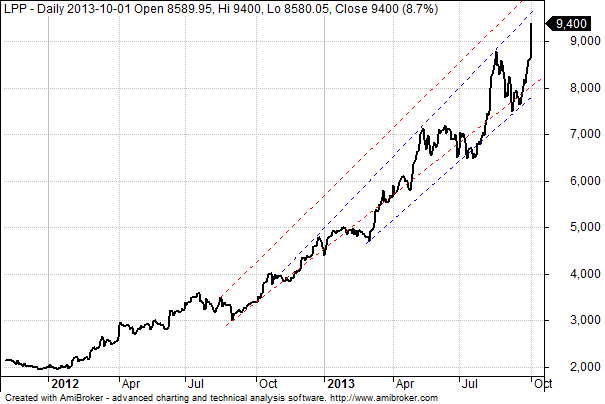
Teraz spójrzmy na ten sam wykres w skali liniowej.
Linie wyrysowane wcześniej pozostały – i już są tym samym całkowicie bezużyteczne. Musimy więc posiłkować się nowymi (na niebiesko). Te już nie są takie zgrabne. Po pierwsze są krótsze, po drugie zaś nie jest to już kanał tylko jakiś rodzaj rozszerzającego się klina. Co więcej poziom wyznaczany przez górne ograniczenie znajduje się niżej, czyli sugeruje znacznie wcześniejsze wyczerpanie bieżącego impulsu wzrostowego.
Naturalnie istnieje całkiem spora rzesza analityków technicznych, którzy uwielbiają na wykresie rysować setki linii, w dziesiątkach ujęć, wykorzystując różne skale cenowe oraz czasowe. Dzięki temu zawsze mogą powiedzieć, że „zdziałał opór lub wsparcie na jednym z trzydziestu wyznaczonych poziomów, co oznacza jego niesłychanie ważne znaczenie”. Jednak minimalistów takie podejście może nie specjalnie satysfakcjonować, zwłaszcza, że przy takim podejściu na wykres możemy rzucić bierki i być pewnym, że któraś z nich zadziała jako ważny opór lub wsparcie (wyobraźcie sobie te możliwości interpretacyjne – opór wyznaczany przez trójząb miałby o wiele większe znaczenie niż wiosło, nie mówiąc już o oszczepach, które można by traktować wyłącznie jako linie pomocnicze przy oznaczaniu trendów mniejszego rzędu).
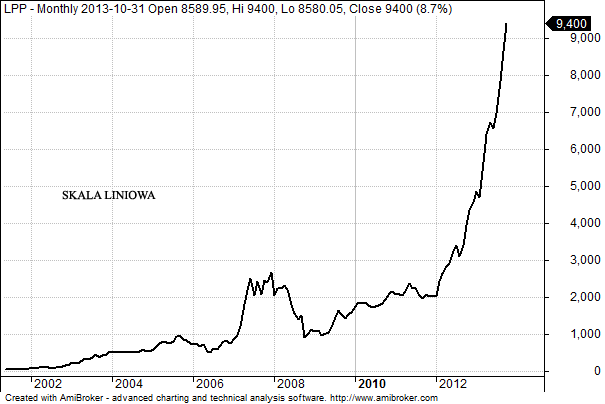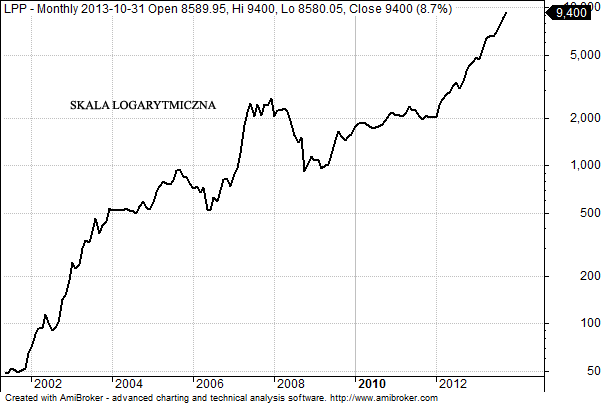
LPP jest skrajnym przypadkiem sytuacji, w której skala liniowa nie pokazuje zbyt wiele. Widać to zresztą doskonale jeśli weźmiemy wykres od początku notowań. Okres 2002 – 2003 można by zdefiniować jako czas, w którym nic się nie działo – ot trend boczny. Jednak w ujęciu logarytmicznym, widzimy wzrost podobnej skali, jak ten, który obserwujemy w ciągu ostatnich trzech lat.
Oczywiście do takiej konkluzji dochodzi wcześniej czy później każdy, kto ogląda wykresy długoterminowe, co nie znaczy że muszą one być przydatne do tradingu w znacznie krótszym horyzoncie.
Inspiracją do napisania tego tekstu była przeczytana przeze mnie informacja, że ujcie logarytmiczne jest naszą uniwersalną intuicją, której pozbywamy się wraz z nabywaniem rożnych umiejętności kulturowych – między innymi korzystając z linijek, miar itp. – gdzie skala przedstawiana jest liniowo.
Na początek wyniki pewnego eksperymentu. Poprosiłem moje sześcioletnie dziecko, żeby na osi, na której końcach narysowane były dwa kółka – na początku zawierające jedną kropkę, a na końcu dziesięć kropek, umieściło pozostałe kółka z kropkami –od dwóch do dziewięciu.
Wynik na obrazku (przepraszam za jakość).
Jak łatwo się zorientować – odległości między kolejnymi punktami są raczej logarytmiczne niż liniowe.
Zupełnie przypadkiem w przedszkolu, do którego chodzi moje dziecię, w jego grupie dzieci miały bardzo podobne zadanie wykonania (tym samym zwiększyła mi się próba badawcza). Ich zadaniem było umieszczenie na osi kolejnych cyfr (doszedł więc element kulturowy) oznaczających dni tygodnia. Wyniki poniżej (ponownie przepraszam za jakość, dane wrażliwe usunąłem):
Rozpiętość wieku uczestników to przynajmniej kilka miesięcy (a w tym okresie ma to spore znaczenie). Widać jednak, że postrzeganie „logarytmiczne” rzeczywistości również w kilku przypadkach się pojawia. Choć co ciekawe przyjmuje ono formę czasami taką jak u mojego syna (mniejsze liczby skupione bliżej siebie), lub odwrotną (im wyższe wartości, tym odległości mniejsze).
Munduruku to siedmiotysięczna grupa rdzennych mieszkańców brazylijskiej Amazonii. W ich języku nie istnieją czasy, nie ma liczby mnogiej, ani liczebników większych niż 5. Tym samym jest to interesująca grupa do badań nad językiem, czy intuicyjnym pojmowaniem liczb. Takimi badaniami zajmował się Pierre Pica (były student Noama Chomskiego). Pica przeprowadzał z nimi eksperyment opisany przeze mnie wyżej jako pierwszy (uporządkuj kropki – Mundruku nie znają liczb).
„Dorośli Amerykanie, wykonując to samo zadanie, umieszczali liczby w równych odstępach na linii. Odtwarzali zapamiętaną ze szkoły oś liczbową, na której sąsiednie liczby znajdują się w tej samej odległości, jakby odmierzono je linijką. Munduruku odpowiadali zupełnie inaczej. Uważali, że odstępy między liczbami na początku są duże, a potem wraz ze wzrostem liczb stają się coraz mniejsze.”
Wyniki badań były dla naukowców na tyle zaskakujące, że zaczęto je powtarzać.
„W 2004 roku Robert Siegler i Julie Booth z Carnegie Mellon University w Pittsburghu przedstawili podobną wersję eksperymentu z osią liczbową grupie dzieci z zerówki (średnia wieku 5,8), pierwszoklasistom (6,9) i drugoklasistom (7,8). Wyniki pokazały w zwolnionym tempie, jak znajomość liczenia kształtuje intuicję. Zerówkowicz bez formalnej edukacji matematycznej sytuuje liczby logarytmicznie. W pierwszym roku nauki szkolnej, gdy uczniowie zapoznawani są z nazwami i symbolami liczb, krzywa zaczyna się prostować. W drugiej klasie liczby są już równomiernie ułożone wzdłuż linii.”
Dlaczego tak się dzieje?
„Pica jest przekonany, że przybliżone pojmowanie ilości w kategoriach szacowania proporcji jest uniwersalną ludzką intuicją. Zresztą ludzie, którzy nie znają liczb (jak Indianie i małe dzieci), nie mają innego wyboru, jak widzieć świat w ten sposób. Pojmowanie ilości w kategoriach precyzyjnych liczb nie jest umiejętnością uniwersalną, lecz wytworem kultury. Pierwszeństwo przybliżeń i proporcji przed precyzyjnymi liczbami, jak sugeruje Pica, wynika z faktu, że proporcje są o wiele ważniejsze dla przetrwania w naturalnych warunkach niż umiejętność liczenia. Mając przed sobą grupę przeciwników uzbrojonych w dzidy, musieliśmy natychmiast wiedzieć, czy jest ich więcej od nas. Kiedy widzieliśmy 2 drzewa, musieliśmy od razu wiedzieć, na którym rośnie więcej owoców. Ani w jednym, ani w drugim wypadku nie było konieczne liczenie każdego wroga lub każdego owocu z osobna. Decydujące znaczenie miała zdolność do szybkiego oszacowania istotnych ilości i porównania ich, czyli inaczej mówiąc, do określenia przybliżeń i oceny ich proporcji.
Skala logarytmiczna wiernie oddaje również sposób postrzegania odległości i pewnie dlatego jest tak intuicyjna. Uwzględnia bowiem perspektywę. Gdy widzimy drzewo w odległości 100 metrów i kolejne 100 metrów za nim, to to drugie 100 metrów wydaje się krótsze. Dla Munduruku idea, że każde 100 metrów reprezentuje taką samą odległość, wypacza to, jak postrzega on otoczenie.
[…]
Nasz głęboko zakorzeniony instynkt logarytmiczny ujawnia się najwyraźniej, kiedy myślimy o bardzo dużych liczbach. Dla przykładu – wszyscy dobrze rozumiemy różnicę między 1 a 10; mało prawdopodobne, byśmy pomylili 1 duże piwo z 10 dużymi piwami. Ale co z różnicą między 1 miliardem galonów wody a 10 miliardami galonów wody? Choć różnica jest ogromna, zwykle postrzegamy obie te wielkości jako dość podobne – po prostu jako bardzo duże ilości wody.”
Niestety w tych opisach nie znalazłem odpowiedzi na pytanie, dlaczego część dzieci porządkuje liczby tak, że najpierw odległości między nimi są bardzo małe, a część (zgodnie z tym co sugeruje Pica i inni badacze) tak, że im wyższa liczba tym mniejsze odległości.
Jeśli jednak ktoś potrzebuje argumentów na rzecz wykorzystywania skali logarytmicznej zamiast liniowej, może spróbować się odwoływać do naszego intuicyjnego rozumienia świata.
Opis eksperymentu, jak również zamieszczone cytaty pochodzą z wyśmienitej książki, opisującej rozwój idei matematycznych „Przygody Alexa w krainie liczb” Alexa Bellosa (wyd. Albatros)
http://www.wydawnictwoalbatros.com/ksiazka,1210,1715,przygody-alexa-w-krainie-liczb.html

26 Komentarzy
Dodaj komentarz
Niezależnie, DM BOŚ S.A. zwraca uwagę, że inwestowanie w instrumenty finansowe wiąże się z ryzykiem utraty części lub całości zainwestowanych środków. Podjęcie decyzji inwestycyjnej powinno nastąpić po pełnym zrozumieniu potencjalnych ryzyk i korzyści związanych z danym instrumentem finansowym oraz rodzajem transakcji. Indywidualna stopa zwrotu klienta nie jest tożsama z wynikiem inwestycyjnym danego instrumentu finansowego i jest uzależniona od dnia nabycia i sprzedaży konkretnego instrumentu finansowego oraz od poziomu pobranych opłat i poniesionych kosztów. Opodatkowanie dochodów z inwestycji zależy od indywidualnej sytuacji każdego klienta i może ulec zmianie w przyszłości. W przypadku gdy materiał zawiera wyniki osiągnięte w przeszłości, to nie należy ich traktować jako pewnego wskaźnika na przyszłość. W przypadku gdy materiał zawiera wzmiankę lub odniesienie do symulacji wyników osiągniętych w przeszłości, to nie należy ich traktować jako pewnego wskaźnika przyszłych wyników. Więcej informacji o instrumentach finansowych i ryzyku z nimi związanym znajduje się w serwisie bossa.pl w części MIFID: Materiały informacyjne MiFID -> Ogólny opis istoty instrumentów finansowych oraz ryzyka związanego z inwestowaniem w instrumenty finansowe.



Fajny tekst.
1. Super zestawienie analityków technicznych i dzieci.
2. W przypadku skali logarytmicznej nie chodzi wyłącznie o intuicję, patrz: Prawo Webera – Fechnera
3. Odnośnie innego postrzegania skali przez Amerykaów i Munduruku, to przeczytaj sobie tę publikację (kiedyś ją podrzucałem nawet, polecam zwłaszcza Jackowi, który za bardzo podjarany jest behawiorystyką):
„The Weirdest People in the World: How representative are experimental findings from American university students? What do we really know about human psychology?”
hci.ucsd.edu/102b/readings/WeirdestPeople.pdf
(autor miał trochę kłopotów ze środowiskiem ‚naukowym’ po napisaniu tej pracy fyi)
Tak czytałem tą notkę i wiedziałem, że skończy się Alexem w krainie liczb.
Napiszę jutro notkę w odniesieniu do tego, bo akurat mam za sobą spotkanie z gościem zrozpaczonym tą dowolnością w stosowaniu skal.
@blackswan
Wroce do tego materiału, bo go zaczynalem i porzucilem gdzieś.
A czy przypadkiem panu Pica nie pomieszały się liczby z cyframi? Przecież:
„Mając przed sobą grupę przeciwników uzbrojonych w dzidy, musieliśmy natychmiast wiedzieć, czy jest ich więcej od nas. Kiedy widzieliśmy 2 drzewa, musieliśmy od razu wiedzieć, na którym rośnie więcej owoców.”
to nic innego, jak definicja liczb naturalnych wg von Neumanna 😉
Moim zdaniem problem może brać się z różnego postrzegania otaczającej nas rzeczywistości. My postrzegamy ją jako dyskretną, złożoną z oddzielnych obiektów, które mogą być policzone. Może Munduruku i dzieci jako ciągłą – materię, którą można zmierzyć. To rozróżnienie pomiędzy liczbami do liczenia a liczbami do mierzenia sięga w głąb naszego sposobu mówienia i myślenia. Na przykład język chiński posługuje się prawie wyłącznie rzeczami, które są mierzone – każdy rzeczownik ma swoje „słowo mierzące” (量词 liàng ci). Być może kultura i edukacja sprawia, że liczenie dominuje w naszym sposobie myślenia.
Przy okazji zagadka: Podobno Jezus Chrystus po trzech dniach zmartwychwstał. Trzech? Ukrzyżowany został w Wielki Piątek, zmartwychwstał w niedzielę… wychodzi, że leżał w grobie tylko dwa dni 🙂
A nie wystarczyłoby proste stwierdzenie faktu: używamy skali logarytmicznej ponieważ (w niektórych dziedzinach niemal wyłącznie)interesują nas zmiany procentowe?
@ osoamoroso
„Zmartwychwstał trzeciego dnia, jak powiada Pismo”, a nie „po trzech dniach”. Jak policzysz z piątkiem, to się zgadza.
@dorota
Samo zainteresowanie zmiany procentowymi nie wystarczą.
Chcąc je nanieść na wykres w skali liniowej otrzymujemy hiperbolę.
Chcąc liniowo porównac zmiany procentowe z róznych układów odniesienia na wykresie musisz zmienić skalę wykresu na logarytmiczną.
Wszystko to odnosi sie do osi Y.
Nikt nic nie wspomina o osi X /czasu/ , która zawsze jest liniowa , a czemuż by nie zrobić jej logarytmicznej wszak im człowiek starszy to czas szybciej leci 🙂
kwestia czasu w ujęciu logarytmicznym jest wspominana w ksiązce Bellosa (dokladnie w tym kontekście)
Pamietam jak lata temu, gdy rysowałem wykresy na papierze milimietrowym, gdzieś zobaczyłem zdjęcie takiego papieru specjalnie do rysowania wykresów w skali logarytmicznej (zwlaszcza ze hossa 93 sprawiala, ze wykres sie nie mieścil).
Bylem zauroczony
A teraz prosze d wyboru do koloru:
http://www.printablepaper.net/category/log
@ Pit
a mówiąc poważnie: zastanawiam się, dlaczego mielibyśmy relacje między kolejnymi liczbami naturalnymi postrzegać logarytmicznie. Przecież jak liczymy jabłka w koszyku, to kolejne nie zmienają nam skali…
Równomierne rozmieszczenie liczb naturalnych na skali poziomej jest jedynym logicznym rozwiązaniem.
PS. Postrzeganie czasu i jego upływu to osobny, fascynujący temat. Nie wiem, jak to jest na starość (i Ty też jeszcze długo nie), ale niekiedy czas rzeczywiście „przyspiesza” lub „spowalnia”. Nie logarytmicznie, ale raczej pulsacyjnie 😉
@_dorota
Apropos jabłek
Podobno nie jestes „liniowym” goldbugiem 🙂
Wierzę tylko w dementi.
Kobietom w dwójnasób.
MOże to jest kwestia perspektywy , w każdym bądż razie trzeba byc konsekwentnym jaką się przyjmie podstawę do wyliczeń .
Najgorsza jest konwersja między systemami co skutkuje np. wysiłkiem narysowania liniowego trendu na nieliniowej skali 🙂
Osobiście skoro oficjalnie liczymy wzrosty procentowo to preferuje skalę logarytmiczną. MAły interwał prawie liniowy,duży lepiej sie trendy rysuje i porównuje fale. Co do spadków to preferuje podejście liniowe bo nigdy nie spadamy do 0 , a procent spadku liczony jest właśnie do tego punktu odniesienia .
@_dorota
„I zaczął ich pouczać, że Syn Człowieczy musi wiele cierpieć, że będzie odrzucony przez starszych, arcykapłanów i uczonych w Piśmie; że będzie zabity, ale po trzech dniach zmartwychwstanie.”, Mar 8:31 za Biblią Tysiąclecia
W oryginale użyte jest μετα τρεις ημερας, więc nie ma wątpliwości, że chodzi o „po trzech dniach”.
Mam nadzieję, że gospodarz bloga wybaczy tę dygresję. Ot, taka ciekawostka pokazująca, że zhellenizowani Żydzi z początku naszej ery inaczej niż my postrzegali czas.
@gzalewski
Myslę ,że zakrzywiac czasoprzestrzeni na wykresie to nie będziemy 🙂
Już sporo nabroił Einstain w tym temacie w fizyce, a twierdząc ,że procent składany jest największym wynalazkiem ludzkości nabroił i w innych dziedzinach na planecie gdzie raczej bardziej swojską miarą jest podziałka liniowa o czym wspominała _dorota w kontekście jabłek.
@osoamoroso
ale jednak w przekłądach jest „trzeciego dnia” to raz.
A dwa – no chyba trzeba by się zastanowić nad statusem 0, ono nie bylo oczywiste 🙂
@pit65
Poprawiać wszędzie na półlogarytmiczny? 🙂
No tak się przyjęło przy tych nieszczęsnych wykresach.
Od czasu do czasu pojawia się nawet pseudologarytmiczny
@ osoamoroso
Może to „po trzech dniach” w cytowanym przez Ciebie fragmencie jest uproszczeniem służącym lepszej redakcji tekstu. Zamiast „w trzecim dniu po zabiciu” napisano „po trzech dniach”, tekst zyskuje na klarowności i rytmie.
Niemniej sam Twój offtopicowy wtręt przypomina, że postrzegamy rzeczywistość przez pryzmat języka, jakim się posługujemy. Pozostaje ogromny obszar nieprzekładalnych niuansów.
@_dorota
„Postrzeganie czasu i jego upływu…”
To jest to samo zjawisko. Masz rację, czas rzeczywiście może przyspieszać i zwalniać. Wrażenie stałego upływu czasu jest złudzeniem i wynika z faktu, że przez całe nasze życie otaczają nas zegary.
Pierwotne kultury nie używają zegarków, więc nie zatraciły zdolności odczuwania czasu – prawdziwej jego natury, czyli oscylacji i pulsacji przestrzeni, która nas otacza.
Ten stan rzeczy odzwierciedla kultura tych ludów, np. muzyka. Dlaczego czujemy się tak „dziwnie” (ożywienie, podniecenie, niepokój, lęk, strach), kiedy słyszymy np. afrykańskie klimaty?
Moim zdaniem, dlatego, że afrykański busz jest po prostu innym wymiarem czasu, gdzie na dodatek płynie on naprawdę bardzo szybko… Z tego też powodu, kiedy słuchamy „śpiewu dżungli”, który jest zapisany w dźwiękach muzyki pierwotnych kultur afrykańskich – w naszych umysłach, przyzwyczajonych do wolnego upływu czasu – owo „tchnienie czasu” powoduje delikatne oszołomienie i zamęt.
Na marginesie, czy naprawdę uważacie, że członek kultury pierwotnej żył krócej od nas, bo umarł w wieku lat 20, zjedzony przez lwa, a my żyjemy znacznie dłużej od niego, bo w spokoju dożywamy 70tki? Biedni…, ów młody bohater, kiedy umierał, był o wiele starszy od całej naszej czeredy spokojnych przeżuwaczy tego, co tam „upolujemy” w „supermarkecie”.
Ale nie tylko ludy pierwotne potrafią odczuwać właściwy upływ czasu. Wydaje się, że niektóre kultury rozwinięte mogły nie zatracić tej zdolności odczuwania zmiennej natury czasu (względnie zatraciły, a potem, na pewnym etapie rozwoju intelektualnego i duchowego, na nowo odkryły), co również znalazło wyraz w ich kulturze:
www.youtube.com/watch?v=fWg6OLqHlNM
Przypuszczam, że również dzieci do pewnego momentu mogą mieć zdolność odczuwania prawdziwej natury czasu. Czyżby te dzieciaki, które rysują mniejsze, a potem coraz większe odstępy – nieświadomie rysowały upływający czas, który w ich wieku zaczyna mocno przyspieszać?
@gzalewski
„no chyba trzeba by się zastanowić nad statusem 0, ono nie bylo oczywiste”
Właśnie! Status 0 chyba nadal jest nieoczywisty. Przypominam sobie spór o to, kiedy rozpoczyna się XXI wiek. Zwolennicy mierzenia czasu twierdzili, że w nocy 31 grudnia 2000 roku; zwolennicy liczenia, których była większość, że 31 grudnia 1999 roku.
A wszystko za sprawą skromnego mnicha Dionysiusa Exiguusa, który w VI wieku dostosowując chrześcijański sposób liczenia lat stworzył kalendarz pozbawiony roku 0 🙂
Ad rem, bo grozi mi popadnięcie w dygresje od dygresji.
Dyskusje na temat wyższości skali logarytmicznej nad liniową są tak samo bezsensowne, co dyskusje na temat wyższości kartezjańskiego układu współrzędnych nad biegunowym. Liczy się jedynie konwencja, użyteczność i wygoda.
@Kornik
Czytałeś „Czarodziejską górę” Manna? Tak mi się jakoś skojarzyło… 🙂
@ osoamoroso
Idę o zakład, że Manna jeszcze na blogach nie było. Jak mawiała niedawno moja córka – wow! Jak się jeszcze pojawi Proust to dojdziemy do ściany….
@astanczak
Wykonajmy zatem ten ostateczny krok. Proust o sztuce przewidywania i stawianiu stop-lossów [spoil alert!]:
„Tak oto pewnego wieczoru list od mojego agenta giełdowego otworzył wrota więzienia, w którym Albertyna żyła nadal, choć tak daleko i tak głęboko, że dla mnie nieosiągalna. Po jej śmierci zaniedbywałem spekulacje podjęte kiedyś z myślą o pomnożeniu pieniędzy, których potrzebowałem ze względu na nią. Lecz oto zmieniły się czasy, a niewzruszone pewniki minionej epoki obaliła ta nowa, podobnie jak kiedyś twierdzenia pana Thiersa, że kolej żelazna się nie przyjmie: najmocniej zniżkowały właśnie te papiery, o których pan de Norpois mówił nam kiedyś: »Może nie gwarantują nadzwyczajnych zysków, ale przynajmniej dają pewność, że kapitał nie stopnieje.« Na samych obligacjach rządu angielskiego i akcjach kompanii naftowych ponosiłem olbrzymie straty, płacąc jednocześnie procent i koszta transakcji prolongacyjnych, aż w odruchu zniecierpliwienia postanowiłem sprzedać wszystko, i wtedy okazało się, że ze spadku po babce została mi ledwie piąta część tego, co miałem jeszcze za życia Albertyny.”, M. Proust, „Utracona”
Ku przestrodze:
„- Czy wiesz, dokąd poszedł Cottard [Cottard był lekarzem – dop. mój]? Jest u Saniette’a, którego manewr giełdowy, mający go ocalić, spalił na panewce. Dowiedziawszy się, że nie ma już ani franka, a ma blisko milion długów, Saniettte dostał ataku.
– Ale też po co grał; idiotyczne, to człowiek najmniej stworzony do tego! Sprytniejsi dają się oskubać, a on był przeznaczony na to, aby go każdy wykierował.
– Ależ rozumie się, od dawna wiemy, że to idiota – rzekł Verdurin. – Ale ostatecznie stało się.”, M. Proust, „Uwięziona”
🙂
Brawo 🙂
Wszystko już było.
@osoamoroso
wg a.stanczaka właśnie przeniknąłeś przez ścianę 🙂
To jest to jedno z wielkich dzieł, z którym nigdy nie było mi po drodze.
Sympatyczne są te odniesienia
Świetny tekst!
Problem natomiast chyba nie tak doniosły – z pewnością warto patrzeć na te same wykresy, na które patrzą inni (poziomy oporu/wsparcia zadziałają tylko wtedy, gdy odpowiednia liczba osób je zidentyfikuje) – a większość patrzy na skalę logarytmiczną 🙂
off topic
@gzalewski
Wasza słynna formacja Batmana zyskuje na popularności 🙂
http://www.fxstreet.com/news/forex-news/article.aspx?storyid=adc208b5-a88a-41f6-9aaa-1cf318fd37e7
A czy z dziećmi nie jest przypadkiem tak, że nie potrafiąc sobie podzielić w głowie odcinka na siedem czy dziesięć różnych części najpierw stawiają pierwszą cyferkę gdzieś tam blisko początku, a potem z każdą kolejną zostaje im mniej elementów do oszacowania tym jest im łatwiej, i wtedy zaczynają „korygować” długości odcinków – albo zmniejszając je, aby się zmieścić, albo zwiększając by nie skończyć uzupełniania zbyt wcześnie. Sam się czasami na czymś takim łapię gdy np. chcę wpisać jakiś wyraz w określone miejsce na papierze – albo zaczynam zbyt gęsto i potem „rozrzadzam” czcionkę, albo odwrotnie – zaczynam zbyt luźno i na koniec muszę zacieśniać litery. Może nie tak bardzo jak małe dziecko, ale jednak.
Tak więc ja bym się w tym nie doszukiwał większego sensu, już wiele teorii związków przyczynowo-skutkowych powstało z powodu nieodpowiedniego rozpoznania wszystkich czynników, które mogą mieć na ten związek wpływ. Tu myślę, że najprostsze rozwiązanie może być prawidłowe. Oczywiście to, że uważam doszukiwanie się u nas wrodzonej zdolności do myślenia w skali logarytmicznej za słabo uzasadnione, nie oznacza, że nie uważam iż przy analizie rynków finansowych takiej skali powinno się używać. Tu jak najbardziej zgodzę się z autorem.
Dobry tekst. Dalsze liczby (wieksze) moga sie znjadowac dla niektorych osob bo roznica miedzy nimi – nie ma takiego znaczenia.
Tak jak powiedzial stalin, jak zabijesz kilka osob to morderstow, jak zabijesz miliony to tylko statystyka.