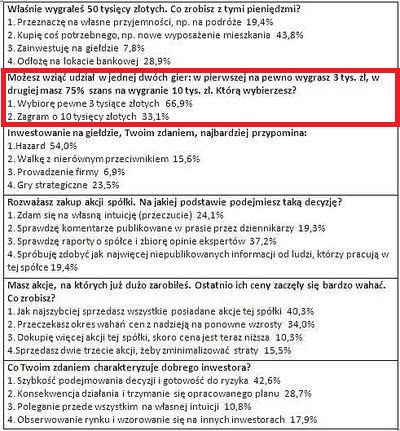
Z Pulsu Biznesu dowiedziałem się o badaniu TNS Pentor dotyczącym inwestycyjnych zachowań i preferencji Polaków. Z badań wynika, że zaledwie 8% Polaków zdecydowałoby się zainwestować na giełdzie nieoczekiwaną wygraną w wysokości 50 tysięcy złotych (29% odłożyłoby ją na lokacie bankowej). To zupełnie zrozumiałe skoro siedmiu na dziecięciu Polaków postrzega giełdę jako hazard (54%) lub grę z nierównym przeciwnikiem (16%).
Mnie zafascynowały odpowiedzi na drugie pytanie w badaniu, w którym zapytano respondentów o decyzję, którą podjęliby mając do wyboru
- scenariusz 1 – pewną wygrana w wysokości 3 tysięcy złotych
- scenariusz 2 – 75% szans na wygranie 10 tysięcy złotych i 25% szans na brak wygranej
Dwie trzecie Polaków wybrałoby pierwszą opcję, czyli ‘pewny zysk’. Proszę zwrócić uwagę, że oczekiwana wartość wygranej w scenariuszu 1 to 3 000 zł a w scenariuszu 2 to 7 500 zł (0,75 * 10 000).
Za Puls Biznesu
Wspomniane badanie Pentoru świetnie ilustruje jeden z postulatów teorii perspektywy Kahnemana i Tversky’ego: ludzie przeważają, przeceniają ‘pewność’ względem opcji, które są ‘tylko’ bardzo prawdopodobne. Występują dwa ‘odwrotne’ fenomeny. Zmierzeni z dwoma bardzo niskimi prawdopodobieństwami zdarzeń ludzie preferują opcję o większej nominalnej wygranej, nawet jeśli wartość oczekiwana tej wygranej (wskutek dużo niższego prawdopodobieństwa) jest niższa. Ten efekt może być odpowiedzialny za zachowanie inwestorów względem śmieciowych akcji.
Gdy ludzie stoją w obliczu możliwości poniesienia pewnej straty (powiedzmy 100% szans na stratę 3 000 zł) i możliwości uniknięcia straty przy ryzyku poniesienia jeszcze większej straty (powiedzmy 80% szans na stratę 4 000 złotych i 20% szans na brak straty) to w istot z wysoką awersją do ryzyka zamieniają się w istoty preferujące ryzyko.
Jeśli przecenianie ‘pewności’ względem opcji, które są ‘tylko’ prawdopodobne występuje na rynku (gdzie powtarzalność ‘gier’ teoretycznie pozwala inwestorom na proces ‘uczenia się’) to może to wyjaśnić możliwość istnienia eksploatowanych nieefektywności na rynku, zwłaszcza na rynku zdominowanym przez inwestorów indywidualnych. Być może wydaje się to sprzeczne z intuicją, jednak wysoka awersja do ryzyka nie zawsze jest postawą optymalną z ekonomicznego punktu widzenia.

30 Komentarzy
Dodaj komentarz
Niezależnie, DM BOŚ S.A. zwraca uwagę, że inwestowanie w instrumenty finansowe wiąże się z ryzykiem utraty części lub całości zainwestowanych środków. Podjęcie decyzji inwestycyjnej powinno nastąpić po pełnym zrozumieniu potencjalnych ryzyk i korzyści związanych z danym instrumentem finansowym oraz rodzajem transakcji. Indywidualna stopa zwrotu klienta nie jest tożsama z wynikiem inwestycyjnym danego instrumentu finansowego i jest uzależniona od dnia nabycia i sprzedaży konkretnego instrumentu finansowego oraz od poziomu pobranych opłat i poniesionych kosztów. Opodatkowanie dochodów z inwestycji zależy od indywidualnej sytuacji każdego klienta i może ulec zmianie w przyszłości. W przypadku gdy materiał zawiera wyniki osiągnięte w przeszłości, to nie należy ich traktować jako pewnego wskaźnika na przyszłość. W przypadku gdy materiał zawiera wzmiankę lub odniesienie do symulacji wyników osiągniętych w przeszłości, to nie należy ich traktować jako pewnego wskaźnika przyszłych wyników. Więcej informacji o instrumentach finansowych i ryzyku z nimi związanym znajduje się w serwisie bossa.pl w części MIFID: Materiały informacyjne MiFID -> Ogólny opis istoty instrumentów finansowych oraz ryzyka związanego z inwestowaniem w instrumenty finansowe.

@Trystero
Podany przez ciebie scenariusz nie jest obarczony ryzykiem ale niepewnością, a to zasadnicza róźnica. Tak naprawdę w jednorazowym zakładzie można wygrać lub wszystko stracić, prawdopodobieństwo nie ma tu nic do rzeczy, jeżeli chodzi o ocenę niepewności.
Co innego, gdyby zadać pytanie – „zagrajmy sto razy ten scenariusz …” wtedy wynik jest już obarczony statystycznym ryzykiem, wtedy już ma sens obliczenie „oczekiwanej” wygranej. Oczywiście wtedy wyniki ankiety pokazały by także zdecydowaną preferencję ankietowanych osób do gry nad „pewną” ale niższą „wygraną”.
@ jacek
Rozumiem ograniczenie eksperymentu, badania wynikające z braku powtarzalności wyboru. Natomiast jednorazowość nic nie zmienia w kwestii oczekiwanej wartości wygranej.
Zastanawiam się też, na ile poszczególnego transakcje na rynku akcyjnym na przykład, są w percepcji inwestorów jednorazowe a na ile są serią.
Badaniu poddano Polaków, a nie wyselekcjonowaną podgrupę inwestorów. Tak sobie myślę, że przeciętny Polak woli pewność wygranej 3000zł z tego prostego powodu, że wyższą wartością oczekiwaną nie wykarmi rodziny… A 3000zł na trochę wystarczy…
Nie uwazam aby decyzja tych dwoch trzecich respondentow byla koniecznie nierozsadna. Uwazam tez, ze porownanie do mechanizmu akcji smieciowych nie musi byc tutaj adekwatne. Zaproponowalbym dodatkowy eksperyment – zaproponowanie respondentom tego samego z tym ze jesli zdecydowalby sie na hazard to gra modbylaby sie 10-krotnie. Jesli respondent zdecydowalby sie sie brak udzialu w grze otrzymalby 10 x 3tys. zlotych albo moglby miec 10 rzutow, w ktorych mialby za kazdym razem 75% szansy na wygranie 10tys. zlotych. W ten sposob znacznie obnizylbym wariancje.
Zwroc uwage, ze z punktu widzenia uzytecznosci 10tys. zlotych niekoniecznie moze sie wydac repondentowi 3x bardziej potrzebne niz 3tys zlotych. Na gre o 10tys. zlotych zdecyduje sie osoba zamozniejsza lub na przyklad osoba, ktora znajduje sie w sytuacji w ktorej 10tys. stanowi ratunek (na przyklad pozwoli wyjsc z pulapki kredytowej), a 3tys tej roli nie spelni. Krotko mowiac na decyzje respondentow moze rowniez wplywac bardzo silnie ich osobista sytuacja, ktora nie moze byc zmierzona za pomoca samej wartosci oczekiwanej z gry.
Mozna tez sie zastanawiac na ile grupa ludzi zajmujaca sie inwestycjami jest w rozkladzie swojego podejscia do gry i ryzyka podobna do calosci populacji.
@Trystero
Moim zdaniem nie ma tu żadnego ograniczenia eksperymentu. Po prostu czym innym jest eksperyment jednorazowej „gry” a czym innym eksperyment serii „gier”. W pierwszym przypadku decyduje niepewność pomiędzy możliwym wynikiem: wszystko – nic, w drugim przypadku możemy mówić o ryzyku i porównywać oczekiwane wartości wygranej. W przypadku serii gier wynik wszystko – nic jest nieprawdopodobny, a w przypaku jednej gry taki wynik jest pewny. Stąd ewidentna i uzasadniona różnica w postrzeganiu tych sytuacji prez „grającego” i w jego oczekiwaniach co do rezultatu „gry”.
Moim zdaniem porównywanie „wartości oczekiwanej” dla jednokrotnej gry nie wyjaśnia preferencji graczy, ponieważ na decyzję gracza silniej rzutuje niepewność i awersja do podejmowania ryzyka niż matematyczne prawdopodobieństwo zdarzenia.
Patrzę sobie na ankietę i tak być powinno:”proza życia” wygrywa z „teoria gier”,a więc wszystko stoi na nogach IMO i nic przeszacowane sie nie wydaje 🙂
Jak to mówi przysłowie aby przeżyć lepszy kanarek w garści jak tłusty indor na dachu czyli innymi słowy wartość oczekiwana.
Skoro tylko:
1. 7% wierdzi ,że inwestowanie jest jak prowadzenie firmy
2. i jedynie 28 uważa ,że trzeba mieć plan do tego
to jak najbardziej odpowiedź na pytanie 3 odpowiada oczekiwaniom respondentów.
Odwracając rozumowanie co by sie stało gdyby 66% dało sie ponieść urokowi pogoni za „wartością oczekiwaną” w sytuacji uwarunkowanej pkt 1 i 2.
Odp: Ani wróbla ni indyka.
Wielka mi zagadka – preferowanie pewnego zysku i nieuświadomiona statystycznie ucieczka od straty. Prawdziwe pytanie brzmi: jak to sprzedać?
Dla człowieka obie wygrane przypadają do tej samej kategorii jakościowej „sporo”. Przy sformułowaniu „Sporo na pewno” czy „Trochę większe sporo albo nic”. Człowiek nie jest bankiem, funkcja użyteczności nie przelicza każdej złotówki na tyle samo satysfakcji.
Proponuję zamienić pytanie na 3zł czy 75% na 10 zł. Mimo że dla teorii rząd wielkości nie ma znaczenia, skłonność do ryzyka będzie bardziej racjonalna. (Co ma dużo sensu, biorąc pod uwagę fakt, że małe kwoty można zyskać lub stracić często; a jeśli nadarzy się okazja na większą wygraną zmarnowanie jej z powodu pecha jest bardziej bolesne)
Można to pytanie zrozumieć też tak: dostajesz 3k. Możesz wziąć udział w „grze” o zasadach: na 25% tracisz 3k, na 75% zyskujesz 7k. Przy tak postawionej kwestii pytanie ogranicza się do stwierdzenia czy lubisz hazard w tej skali pieniędzy jeśli kostka jest po twojej stronie.
Nie wydaje mi się żeby wyliczenie wartości oczekiwanej miało dużo sensu jeśli nie jest to sytuacja powtarzalna.
Inna sprawa że w praktyce rzadko zna się prawdopodobieństwa w wystarczającym stopniu żeby sobie przeliczyć i intuicja unika ryzyka; co wydaje się mieć sens biorąc pod uwagę fakt, że nawet dużą wygraną łatwo zmarnować, a długi są problematyczne.
Przy okazji:
http://pl.wikipedia.org/wiki/Paradoks_petersburski
Nawet skrajnie popsuta teoretycznie gra o nieskończonej wartości oczekiwanej w praktyce nie jest aż taka fajna.
Co do zastosowania praktycznego awersji do ryzyka to ogranicza ona np wygrane w teleturniejach typu Milionerzy. Często nawet jeśli statystycznie jest to nieopłacalne gracze rezygnują z ryzyka.
@ Trystero
„Dwie trzecie Polaków wybrałoby pierwszą opcję, czyli ‘pewny zysk’. Proszę zwrócić uwagę, że oczekiwana wartość wygranej w scenariuszu 1 to 3 000 zł a w scenariuszu 2 to 7 500 zł (0,75 * 10 000).”
Czy jesteś całkiem pewny, iż wartość oczekiwana tej gry wynosi 75k?
Czy czasem nie należy rozpatrywać jej opłacalności biorąc pod uwagę oba scenariusze łącznie a nie rozpatrywać ich oddzielnie?
PS
Jak bardzo trafnie zauważył Zephyr, odpowiedź może być różna gdy zmieni się parametry (wartość wygranych) nie zmieniając samej istoty gry.
„Proponuję zamienić pytanie na 3zł czy 75% na 10 zł. Mimo że dla teorii rząd wielkości nie ma znaczenia, skłonność do ryzyka będzie bardziej racjonalna. (Co ma dużo sensu, biorąc pod uwagę fakt, że małe kwoty można zyskać lub stracić często; a jeśli nadarzy się okazja na większą wygraną zmarnowanie jej z powodu pecha jest bardziej bolesne)”
Ja ze swojej strony proponuję wziąć pod uwagę inny scenariusz:
Pewna kwota 1 miliona do reki lub gra o 10 milionów z szansami 90%.
Zakładam się, że duża grupa respondentów weźmie melona.
Myślę, że da się na te zagwozdki odpowiedzieć bez uciekania się to teorii Kahnemana i Tverskego.
@ lesserwisser
Czy czasem nie należy rozpatrywać jej opłacalności biorąc pod uwagę oba scenariusze łącznie a nie rozpatrywać ich oddzielnie?
Nie, porównujesz wartość oczekiwaną w scenariuszu 1 i w scenariuszu 2 i sprawdzasz gdzie jest większa.
@ hmmmmmmmmm
Oczywiście, to jest fundament teorii Kahnemana i Tversky’ego. Natomiast poszczególne paradoksy pokazują, że funkcja użyteczności u homo oeconomicus ma dość ‚dziwaczny’ kształt bo Ci sami ludzi są jednocześnie miłośnikami ryzyka i mają dużą awersję do ryzyka, w zależności od okoliczności.
@ jack
A to jest bardzo fascynująca uwaga.
Czytałem niedawno na przykład ewolucyjne wyjaśnienie fenomenu ‚dążenia do przechytrzenia prawdopodobieństwa’. W eksperymencie gdzie ludzie mają wskazać, w którym z dwóch pudełek będzie jedzenie (proces jest losowy ale w pudełku 1 jedzenie pojawia się częściej, na przykład 75% czasu) ludzie cały czas próbują zgadywać. Częściej zgadują pudełko 1 (około 75% czasu) ale zgadują zamiast zawsze stawiać na pudełko 1.
Andrew Lo z MIT tak to skomentował:
This strange and well-known example of irrationality in human judgment may not be so irrational after all when viewed from the perspective of evolutionary biology (Lo and Brennan, 2009). To see why, consider the hypothetical case of animal deciding whether to build its nest in a valley or on a plateau. If the weather is sunny, nesting in the valley will provide shade, leading to many offspring, whereas nesting on the plateau provides no cover from the sun, leading to no offspring. However, the opposite is true if the weather is rainy: the valley floods, hence any offspring will drown in their nests, but nests on the plateau survive, yielding many offspring. Now suppose the probability of sunshine is 75% and the probability of rain is 25%. The “rational” behavior for all individuals to follow is to build their nests in the valley, for this maximizes the expected number of each individual’s offspring. Suppose the entire population exhibits such individually optimal behavior—the first time there is rain, the entire population will cease to reproduce, leading to extinction. Similarly, if the entire population behaves in the opposite manner, always choosing the plateau, the first time sunshine occurs, extinction also follows. Lo and Brennan (2009) show that the behavior that maximizes the growth of the population is for individuals to randomize their nesting choice by choosing the valley with probability 75% and the plateau with 25% probability. Matching probabilities confers an evolutionary advantage, not for the individual, but rather for the population as a whole. And since, by definition, the current population consists of the survivors, it will reflect such advantageous behavior disproportionately to the extent that behavior is heritable. While probability matching is, indeed, irrational from the perspective of maximizing an individual’s expected wealth, its evolutionary advantage is clear.
fakt, pojecie funkcji uzytecznosci pojawilo sie juz w XVIII wieku bodajze
@Zephyr
W sumie to temat, ktory zarzuciles, bardzo mocno zahacza o filozofie – paradoks petersburski jest bardzo ciekawy, wielkie dzieki za dygresje w ktorej o nim wspomniales 🙂
odwdziecze sie nastepujacymi linkami:
http://plato.stanford.edu/archives/fall2004/entries/paradox-stpetersburg/
Bardzo polecam ten tekst. Pod nim zlinkowany jest inny, rownie ciekawy:
http://www.ccs.fau.edu/~liebovitch/complexity-20.html
ps. im dluzej zajmuje sie handlem, tym bardziej rosnie we mnie chec glebszego poznania filozofii 🙂
Nie ma nic dziwnego w tego typu zjawiskach (cognitive biases). Obecnie żyjący ludzie pod względem neuronalnych mechanizmów dokonywania wyborów znajdują się nadal na etapie grup łowiecko-zbieraczych sprzed dziesiątków tysięcy lat. Pieniądze to dość nowy wynalazek, ale jeśli jednak weźmiemy pod uwagę pierwotny powód wyewoluowania tego typu przystosowań i zanalizujemy dostęp do pokarmu, to stają się one w pełni zrozumiałe (zwiększają osobniczy fitness). Dla naszego przodka, który zmagał się z niedoborem żywności na sawannie awersja do ryzyka (risk aversion) miała głęboki sens, główne znaczenie miał pokarm dostępny tu i teraz (głód i brak pokarmu określają zachowanie). Myślenie o dalszej przyszłości nie miało więc sensu. Również, w przeciwieństwie do pieniędzy, pokarm nie jest zasobem liniowym tzn. posiadanie dwukrotnie większej ilości pokarmu nie jest tak samo wartościowe jak w przypadku pieniędzy. Żywność może się popsuć i stać niezdrowa, tak więc człowiek jest w stanie spożyć jedynie ograniczoną jej ilość, a nadmiar przestaje mieć znaczenie – mechanizm wciąż znajdujący swoje odbicie w dzisiejszych zachowaniach ekonomicznych.
Poza tym warto zauważyć, że ludzki mózg nie jest właściwie przystosowany do dokonywania wyborów wymagających analiz matematycznych czy znajomości rachunku prawdopodobieństwa. Kahneman i Tversky przeprowadzili m.in takie doświadczenie.
Mamy kostkę sześcienną, której dwie ściany pomalowane są na czerwono (R), a cztery na zielono (G). Wykonujemy 20 rzutów kostką. Poniżej 3 sekwencje potencjalnych częściowych wyników (jedna z nich rzeczywiście się zdarzyła). Zadaniem biorących udział w doświadczeniu było wybranie najbardziej prawdopodobnej sekwencji:
1) R-G-R-R-R
2) G-R-G-R-R-R
3) G-R-R-R-R-R
65% badanych wybrało odpowiedź 2 jako najbardziej prawdopodobną, a jedynie 33% wybrało prawidłową odpowiedź 1.
Dużo zależy od funkcji użyteczności decydenta 😛 Skłonność do ryzyka można różnie interpretować, ale obiektywnie gracz(inwestor) jest skłonny do ryzyka jeżeli jego funkcja użyteczności rośnie szybciej od liniowej.
np jak U1(3000)=3000 a U1(loteria)= 0.75*10 000 + 08.., a U2(3000)=(3000) do potęgi np 1/5, to wyjdzie U2(300)= 4,96, a U2(loteria)= 0.75*(10000 do 1/5)= 6.3*0.75=4,732, a więc dla gracza o dużej awersji do ryzyka wybór wygląda inaczej, bo woli pewne 3k niż loterie (pomimo, że dla innego gracza loteria byłaby atrakcyjniejsza, tzn takiego, który miałby szybciej rosnącą funkcję użyteczności). No i też jest takie zjawisko, że funkcja użyteczności rzeczywista nie jest tak oczywista, tj np niemal dla każdego różnica pomiędzy 2 a 200 pln będzie duża, a dla 1 mld a 2 mld praktycznie żadna, tj jakby zrobić podobną loterię jak wyżej- mniejsza kwota pewna druga z jakimś tam prawdopodobieństwem różnym od 1, to w pierwszej raczej będą ludzie wybierać loterię, a w drugim przypadku pewne 1 mld 🙂
@ Jack
Moge prosić o wyjaśnienie tego przykładu? Skoro prawdopodobieństwo wyrzucenia G jest dwukrotnie większe niż R, to na chłopski rozum ta sekwencja jest najbardziej prawdopodobna, gdzie G jest najliczniej reprezentowane. Gdzie się mylę?
@ dorota
W pierwszym jest 5 rzutów 🙂
@ Trystero
lw- Czy czasem nie należy rozpatrywać jej opłacalności biorąc pod uwagę oba scenariusze łącznie a nie rozpatrywać ich oddzielnie?
T – Nie, porównujesz wartość oczekiwaną w scenariuszu 1 i w scenariuszu 2 i sprawdzasz gdzie jest większa.
Nie jestem tego taki pewny, że jest aż tak prosto, powinno się bowiem wziąć pod uwagę wiele czynników, prawdopodobieństwo zdarzenia, wielkośc rozrzutu wyników, prawdopodobieństwo zdarzenia porównawczego, ewentualne całościowe rozpatrywanie problemu szans i wielkości realnych wygranych.
Prosty przykład: pewne 30k i możliwośc wygrania 150k z prawdopodobieństwem 40%. Wartośc oczekiwana II to 60k, dwa razy większa, ale szansa wygranej jest mniejsza niż połowa.
Czyli częściej przegramy niż wygramy, co w grach losowych bywa przesłanką odrzucania takich strategii.
No bo weźmy trzeci wariant, pewne 30k, szansa na 200k z prawdopodobieństwem 20%. Wartośc oczekiwana 40k a więc niby większaa większa, ale też szansa na wygransa na wygraną jest cztery razy mniejsza niz na przegraną 20% do 80%.
Szanas 1% na 10 milionów daje nam wartośc oczekiwaną 100k – a kto rozsądny to wybierze?
To takie uwagi pod rozwagę, bo problem nie jest wcale taki oczywisty jak się pozornie wydaje.
Ciekawe jak wygląda korelacja między odpowiedziami, w szczególności czy pokrywa się podejście do ryzyka w pytaniach 2. i 5. Rzuciłoby to trochę światła, ile z tych 66,9% ma awersję do ryzyka, a ile do straty.
@ Trystero
Wybacz tą swoistą uporczywość, ale nawet po tym wyjaśnieniu myślę, że sekwencja 2.
Prawdopodobieństwo G/R jest jak 2/1. W sekwencji 1) mamy 1/4, w 2) 1/2, w 3) 1/5. Sekwencja 2 jest najbliższa „modelowej” 2/1.
@ dorota
Po prostu policz sobie prawdopodobieństwo wyrzucenia tych dwóch serii na zasadzie 0,33 * 0,66 i tak dalej.
wszystkim, ktorzy chca sobie usystematyzowac swoja wiedze, tudziez jej kompletny brak, w kwestii prawdopodobienstw i ich mozliwych interpretacji polecam nastepujacy tekst:
http://plato.stanford.edu/entries/probability-interpret/
oczywiscie, wypada wiedziec jak obliczyc prawdopodobienstwa podane w przykladzie Jack’a zanim zacznie sie czytac cokolwiek wiecej…
ps. link powyzszy rzuca tez sporo swiatla na czesto idiotyczne wykorzystywanie w zyciu codziennym pojec ‚wartosci oczekiwanej’ w oparciu o aksjomaty Laplace’a w odniesieniu do zbiorow niepoliczalnych i nieskonczonych
@ dorota
Zwróć uwagę jeszcze na jeden szczegół. Sekwencja 1 zawiera się w sekwencji 2 co załatwia problem tego co jest bardziej prawdopodobne. Tak chyba zresztą Kahneman wyjaśniał dlaczego nigdy nie powinno się wskazywać 2.
@ Trystero
Tak, masz rację. Dzięki.
@ dorota
Trystero ma rację pisząc o tym, że sekwencja 1 zawiera się w sekwencji 2. Prawdopodobieństwo zdarzenia A i zdarzenia B zachodzących równocześnie jest niższe (lub równe) niż prawdopodobieństwo zajście tylko zdarzenia A. Ludzie nie myślą w ten sposób (dobór naturalny nie działał w tym kierunku), stąd masowa wręcz ilość błędów tego typu (cognitive biases), które niestety popełniamy i to nie tylko na rynku).
Spójrz na podobny przykład:
What do you think is more likely to be true about my friend Robert: (A) he is a professional NBA player, or (B) he is a professional NBA player and is over six feet tall?
Większość ludzi wybierze odpowiedź B, chociaż jest ona mniej prawdopodobna niż A.
Jeśli kogoś interesuje ten temat to polecam następujące książki:
„Brain Bugs” – Dean Buonomano
„Predictable Irrational” – Dan Ariely (jest polskie tłumaczenie)
„The Upside of Irrationality” – Dan Ariely
„The Believing Brain” – Michael Shermer
„The Invisible Gorilla” – Christopher Chabris, Daniel Simons
(Doświadczenie z niewidzialnym gorylem jest jednym z najbardziej znanych doświadczeń ostatnich lat. Pokazuje, że w przypadku czegoś nawet tak trywialnego jak zwykła percepcja wzrokowa 50% ludzi nie widzi osobnika przebranego za goryla. Jeśli wiadomo, że zmienność zachodząca na rynku oraz ilość parametrów które należy brać pod uwagę przy podejmowaniu decyzji jest nieporównywalna z percepcją wzrokową lub wręcz leży poza możliwościami naszego mózgu (ewolucyjny determinizm), to niezwykle trudno jest uniknąć błędów przy dokonywaniu wyborów inwestycyjnych.
„Jeśli wiadomo, że zmienność zachodząca na rynku oraz ilość parametrów które należy brać pod uwagę przy podejmowaniu decyzji jest nieporównywalna z percepcją wzrokową lub wręcz leży poza możliwościami naszego mózgu (ewolucyjny determinizm), to niezwykle trudno jest uniknąć błędów przy dokonywaniu wyborów inwestycyjnych.”
enter ockham’s razor…
poza tym ze powyzszego zdania wynikaloby, ze jednak opieranie sie na tej calej masie parametrow, mimo ze zgodnie z przytoczonym przez Ciebie ewolucyjnym determinizmem jest to niemozliwe, jest wskazane, tj. raczej poprawia nasze wyniki niz nie. Trudne stwierdzenie
Przyjmijmy, że informacja jest parametrem, który tu właśnie rozważamy.
Przykład z życia wzięty (podaję za „Invisible Gorilla”).
The same thing happens in the real world of investing decisions. Brad Barber and Terrance Odean managed to obtain six years of trading records for sixty thousand accounts from a brokerage firm and compared investment returns between people who bought and sold stocks frequently and those who traded rarely. Presumably investors who make lots of trades believe that they have lots of knowledge and good ideas about stocks—that each of their trades will make money because it is anticipating a market move. But once their returns were adjusted for the costs and tax payments generated by all the trades they made, the most active traders earned one-third less per year than the least active ones.
A tu doświadczenie przeprowadzone przez ekonomistę behawioralnego, Richarda Thalera:
You are told that you are in charge of managing the endowment portfolio of a small college and investing it in a simulated financial market. The market consists entirely of just two mutual funds, A and B, and you start with a hundred shares that you must allocate between the two. You can put all of your shares into A, all of them into B, or some into A and the rest into B. You will be running the portfolio for twenty-five simulated years. Every so often, you will be informed of how each fund has performed, and thus whether your shares have gone up or down in value, and you will then have the opportunity to change how your shares are allocated. At the end of the simulation, you will be paid an amount that is proportional to how well your shares have performed, so you have an incentive to do as well as you can. Before the game begins, however, you have to choose how often you would like to receive the feedback and have the chance to change your allocations: every month, every year, or every five years (of simulated time).
The correct answer seems obvious: Give us information, and let us use that information, as often as possible! Thaler’s group tested whether this intuitive answer is right—not by giving people the choice, but by randomly assigning them to receive feedback monthly, yearly, or every five years. Most people initially tried a 50/50 allocation between the two funds since they knew nothing about which might be better. As they got information about the performance of the funds, they shifted their allocations. Since the simulated length of the experiment was twenty-five years, the subjects in the five-year condition got feedback and could change their allocations only a few times, compared with hundreds of times for the subjects in the monthly condition. By the end of the experiment, subjects who only got performance information once every five years earned more than twice as much as those who got monthly feedback.
co do pierwszego przykladu – do tego nie trzeba zadnych badan, to jest niby oczywista oczywistosc, sam naleze do ludzi z ADHD jesli chodzi o liczbe wykonywanych transakcji, ale taki mam styl 🙂
chociaz z drugiej strony gdyby przeprowadzic takie badania na rynkach o wiekszej zmiennosci (wybrac tylko okresy z day-to-day vol na poziomie np 40% plus) wtedy wyniki moga byc zgola inne…
co do drugiego przykladu byl identyczny eksperyment zacytowany przez nie-powiem-kogo w swojej nie-powiem-jakiej ksiazce:
Show two groups of people a blurry image of a fire hydrant, blurry enough for them not to recognize what it is. For one group, increase the resolution slowly, in ten steps. For the second, do it faster, in five steps. Stop at a point where both groups have been presented an identical image and ask each of them to identify what they see. The members of the group that saw fewer intermediate steps are likely to recognize the hydrant much faster. Moral? The more information you give someone, the more hypotheses they will formulate among the way, and the worse off they will be. They see random noise and mistake it for information.
moral jest taki: nie ogladajcie CNBC, nie czytajcie dziennikow finansowych bo to jest jedynie szum informacyjny w zaden sposob nie pomagajacy osiagac dobrych wynikow. Dzisiejszy spike na DAX i SP byl tego imo doskonalym przykladem…
Rozpatrując wybór mamy:
1)=3000
Wartość oczekiwaną 3000 dla punktu 1 i to jest odniesienie drugiej inwestycji:
2)+7000*0,75-3000*0,25=4500
Punkt 1 daje pewny zysk 3000 a drugi jest obarczony ryzykiem straty tych 3000 w alternatywie do zysku 7000 z prawdopodobieństwami.
Dodatkowo postawienie kogoś przed tylko jedną szansą ze znaczącą kwotą nawiązuje do całości czegoś co mamy (wyizolowany jeden wybór). Przecież szans nie będzie 1000 więc lepiej nie ryzykować. Statystykę to można zapiąć w stosunku do wyborów powtarzalnych a jednorazowe straty się raczej ubezpiecza.