Jeszcze jedno małe studium na temat czytania ?equity curve” (to drugie czytać ‚kerv’ co znaczy krzywa, nie inaczej) i oceny przebiegów oraz anomalii, które się za nią kryją. To póki co ostatni wpis na temat podstawowych mierników efektywności tradingu i mam nadzieję, że to wystarczy by zrozumieć statystyczne raporty, które pokażą się w przyszłych wpisach.
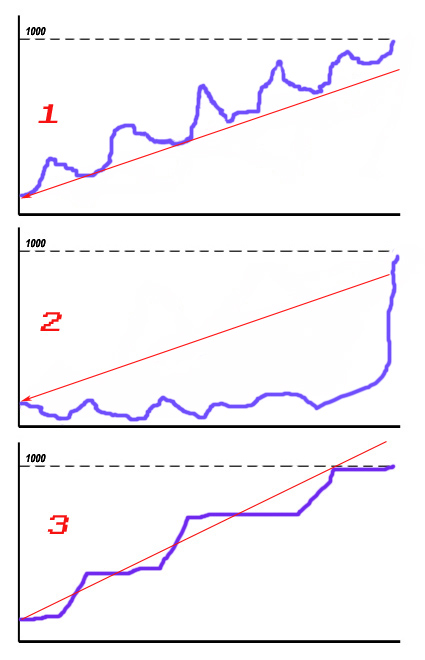
Proszę spojrzeć sokolim okiem na krzywe 3 strategii poniżej. Co je łączy z całą pewnością to końcowy wynik, identyczny zakres czasowy, ten sam instrument oraz jednakowy wskaźnik Sharpe’a (zysk średni dzielony przez odchylenie standardowe). Pozostawiam czytelników w krótkiej kontemplacji by niżej wyjaśnić tajemnice ukryte w tych wykresach.
Wprawdzie wszystkie trzy wyrysowałem ręcznie i może nie są nazbyt perfekcyjnym obrazem rzeczywistości ale mam nadzieję, że krótki opis pozwoli zrozumieć zamierzoną intencję. A chodzi o skrajnie niesymetryczne przebiegi zysków i strat, które mimo to generują taką samą wielkość Sharpe Ratio.
Zaczynając od rysunku nr 1 – niemal wszystkie wartości zmian kapitału leżą ponad czerwoną kreską, która wskazuje pewną tendencję rosnącą. To przybliżony obraz systemu, który oddaje rynkowi spore części z wypracowanych wcześniej zysków ale nie zanurza się zbyt głęboko w stop lossy. Może to być na przykład długoterminowy system podążający za trendem z szerokimi stopami (trailing stops). Owe stopy powodują, że próbując złapać jak największą część trendu, pozycji nie zamyka się na samych ekstremach papierowych zysków osiągniętych w międzyczasie. Tu zawsze są spore wahania od osiągniętych nowych szczytów kapitału. O ile większość zysków rozkłada się powyżej średniej to mamy do czynienia z tak zwaną ?dobrą zmiennością”.
Zupełnie przeciwnie wygląda to z krzywą na rysunku nr.2, która leży skrajnie poniżej czerwonej linii tendencji. Tu obsunięcia są bardzo ?defensywne” bo ta strategia walczy nie po stronie zysków ale głównie odrabia początkowe straty. Zmienność czyli odchylenie standardowe (rozproszenie wokół średniej) jest w przybliżeniu takie same jak w poprzednim przypadku ale ryzyko pozostaje ?subiektywnie” większe, mimo takiego samego zysku końcowego. Wyciąganie z dołków może bowiem teoretycznie dużo szybciej pogrążyć strategię niż oddawanie częściowych zysków. Mamy wówczas do czynienia ze „złą zmiennością”
Trzecia krzywa to nieco inny przypadek. Tutaj strat niemal nie notuje się wcale, są dłuższe okresy braku pozycji i braku ruchów rynku (to te płaskie przebiegi) oraz nagłe, zyskowne zrywy w górę. Tutaj trafność sięga niemal 100% choć zysk końcowy jest taki jak w obu wykresach wyżej i złej zmienności jest niewiele.
Aby zmierzyć te dolne, niepożądane odchylenia, używa się miernika zwanego Sortino Ratio, które powstało bezpośrednio z wzoru na Sharpe Ratio. Różni je tylko mianownik:
Sortino = (Rs – Rf) / ?(d)
W rozwinięciu:
Wskaźnik Sortino = (Średni Zysk – Zysk wolny od ryzyka) / Odchylenie Standardowe dolne
I tu czasem pomija się zysk wolny od ryzyka i pozostaje jedynie:
Sortino = Rs / ?(d)
Sharpe bierze pod uwagę odchylenie standardowe z obu stron średniej, Sortino tylko to poniżej niej. W szczegółach Sortino Ratio wygląda tak, że dla każdego okresu liczenia średniego zysku i odchylenia to ostatnie przyjmuje się jako zero (0) jeśli rozproszenie wyników (fachowo określane jako wariancja) mieści się powyżej średniej lub wartość ujemną, gdy wynik opada poniżej średniej.
Rzadko się liczy Sortino Ratio w systemach, nie ma ono tutaj aż tak wielkiego znaczenia, jest często mocno skorelowane z Sharpe. Oczywiście idealnie jest ową dolną zmienność utrzymać w jak najmniejszym rozmiarze ale mając wgląd do systemu i znając jego założenia wiemy czego można się po ewentualnych wahaniach spodziewać. Natomiast liczy się je dla celów porównawczych, na przykład funduszy lub zarządzanych portfeli, po to by sprawdzić jak menadżer zarządzający radzi sobie z kontrolą ryzyka. Tak jak w Sharpe Ratio i tutaj im większa wartość tym portfel teoretycznie mniej ryzykowny albo raczej mniej zmienny po stronie strat. To ma spore znaczenie dla klientów o czym chyba przekonywać nie ma potrzeby. Porównując fundusze o podobnych parametrach lepiej wybrać oczywiście ten o większym Sortino Rate. Na przykład zabezpieczenie portfela akcji na rynku derywatów powinno zredukować ową dolną zmienność. Jest to więc poniekąd miara klasy zarządzającego.
I mała dygresja na koniec – w wypadku funduszy używa się w pierwszym wzorze podanym wyżej zamiast stopy wolnej od ryzyka minimalną akceptowaną przez inwestora stopę zwrotu, którą niestety nazywa się również MAR od Minimum Acceptable Return – to na wypadek gdyby ktoś potknął się na tym i zdziwił się zbieżnością z MAR, opisywanym wcześniej. Również odchylenie standardowe liczy się wówczas nie od średniej ale od owej minimalnej stopy zwrotu.
–* Kathay *–

3 Komentarzy
Dodaj komentarz
Niezależnie, DM BOŚ S.A. zwraca uwagę, że inwestowanie w instrumenty finansowe wiąże się z ryzykiem utraty części lub całości zainwestowanych środków. Podjęcie decyzji inwestycyjnej powinno nastąpić po pełnym zrozumieniu potencjalnych ryzyk i korzyści związanych z danym instrumentem finansowym oraz rodzajem transakcji. Indywidualna stopa zwrotu klienta nie jest tożsama z wynikiem inwestycyjnym danego instrumentu finansowego i jest uzależniona od dnia nabycia i sprzedaży konkretnego instrumentu finansowego oraz od poziomu pobranych opłat i poniesionych kosztów. Opodatkowanie dochodów z inwestycji zależy od indywidualnej sytuacji każdego klienta i może ulec zmianie w przyszłości. W przypadku gdy materiał zawiera wyniki osiągnięte w przeszłości, to nie należy ich traktować jako pewnego wskaźnika na przyszłość. W przypadku gdy materiał zawiera wzmiankę lub odniesienie do symulacji wyników osiągniętych w przeszłości, to nie należy ich traktować jako pewnego wskaźnika przyszłych wyników. Więcej informacji o instrumentach finansowych i ryzyku z nimi związanym znajduje się w serwisie bossa.pl w części MIFID: Materiały informacyjne MiFID -> Ogólny opis istoty instrumentów finansowych oraz ryzyka związanego z inwestowaniem w instrumenty finansowe.

Ciekawie i przystępnie to opisujesz, ale tak czy owak niezależnie od różnych ratio obowiązuje zasada: duży zysk = duże ryzyko , małe ryzyko = mały zysk.
CAGR%= 38%, MaxDD 2% z poprzedniego wpisu to chyba tylko w Erze 😉
Odnośnie tych equity to nasunęło mi się jeszcze spostrzeżenie, że equity nr 1 i nr 3 mogą być z tego samego systemu, tylko że nr 1 z otwartych pozycji a nr 3 z zamkniętych.
Mając np. do dyspozycji listę transakcji można łatwo zrobić wykres equity, ale z zamkniętych pozycji, bez uwzględnienia DD na pozycjach otwartych.
Co to w praktyce oznacza „odchylenie standardowe dolne” ? czy to oznacza odchylenie standardowe wartości bezwzglednych ale tylko z ujemnych stóp zwrotu budujących ciąg dziennych stóp zwrotów potrzebnych do obliczenia odchylenia st?
Tak , chodzi o odchylenie dla stóp zwrotu poniżej średniej