Procent rozłożony (choć nie w pełni)

Podobno Albert Einstein powiedział, że ?największym wynalazkiem ludzkości jest procent składany?. Można dodać przy okazji, że spora część ludzi posługująca się tym hasłem w celu uzasadnienia inwestycji w akcje, jako najlepszego z możliwych wyborów inwestycyjnych (lub promujących rożnego rodzaju inwestycje) zdanie wypowiedziane przez fizyka rozumie tak dobrze, jak teorię względności.

Przyjrzyjmy się na czym polega cud procentu składanego. Przyjmijmy, że co roku zarabiamy na jakiejś inwestycji 20 procent, rozpoczynając od 1000 zł. Ponieważ każdego roku owe 20 procent jest naliczane od coraz większej kwoty, po 10 latach mamy 6 192 złotych, zaś po dwudziestu 31 948 złotych.

Cud jest jeszcze bardziej cudem, gdy co roku będziemy dokonywali systematycznej wpłaty. Czyli przez dziesięć lat w sumie nasza inwestycja pochłonie 10 000 złotych, zaś przez dwadzieścia lat ? 20 tysięcy. W pierwszym wypadku będziemy posiadali 32 150 zł (3 razy więcej niż wpłaciliśmy). W drugim 225 025 złotych.

To wystarcza, żeby rozbudzić wyobraźnię. Długi termin plus systematyczne zysk. Oto przepis na sukces. Różnią się tylko kwoty podawane jako stopa procentowa możliwa do osiągnięcia.

Gdy startowały fundusze emerytalne w symulacjach przyjmowało się 14-20 procent. Obecnie oczekiwania są skromniejsze i wynoszą 8-12 procent. Nieznany u nas zupełnie Jacob Raskob opublikował w magazynie ?Ladies? Home Journal? materiał pod tytułem ?Każdy powinien być bogaty? (?Everybody Ought to be Rich?). W artykule wykazywał, że inwestując 15 dolarów miesięcznie w akcje przez dwadzieścia lat, możemy oczekiwać 24 procent rocznie i spodziewać się szczęśliwego życia milionera emeryta.

Czy dodałem, że tekst ukazał się w magazynie dla Pań w sierpniu 1929 roku? Kilka miesięcy przed krachem. Brzmi nad wyraz znajomo.

No, ale przecież to było tak dawno. Raskob poczynił założenie 24 procent zysku co roku bazując na ówczesnych danych (później statystyka uległa znaczącemu pogorszeniu, ale skąd mógł o tym wiedzieć). Często się zastanawiałem, czemu u nas nie bazuje się na statystykach z rynku akcji. W końcu giełda istnieje już kilkanaście lat spokojnie można policzyć średnią roczną.

Tu chyba bierze górę rozsądek ?symulatorów?. Średnioroczna stopa zwrotu indeksu WIG od 1991 roku wynosi około 80 procent. W taki wynik nie uwierzy nawet najbardziej optymistycznie nastawiony zwolennik akcji, jako inwestycji. Zwykle mówiło się wówczas, że Wielka Hossa z lat 1992-1993 była niereprezentatywna. Wartość indeksu wzrosła blisko dwudziestokrotnie (dla porównania przez ostatnie cztery lata ?zaledwie? pięciokrotnie). No dobra, zróbmy to co robi się zwykle w takich przypadkach ? znajdźmy liczby, które brzmią bardziej przekonująco. Jest! Indeks WIG20 ? działa od 1994 roku czyli już ?poza czasem nienormalnym?. Średnia roczna stopa zwrotu do końca 2006 roku wyniosła 13.6% To jest liczba, która brzmi wiarygodnie! W końcu cóż trudnego jest w zarabianiu zaledwie 13,6 procent rocznie.

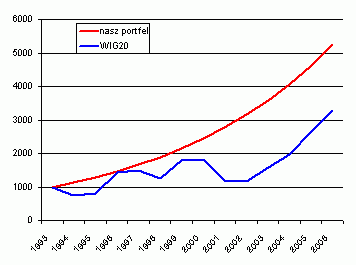
Wpłacając 1000 złotych, po pięciu latach powinniśmy mieć 1891 zł, po dziesięciu 3579 zł, a po trzynastu 5247 zł !!!. Fantastycznie jesteśmy lepsi niż indeks WIG20!!! Rozpoczął na poziomie 1000 pkt,. a po trzynastu latach (koniec 2006) wyniósł 3286 pkt. Rację miał Einstein mówiąc o genialnym wynalazku. Zarabiamy średnio tyle co indeks, a wynik mamy lepszy o ponad 50 procent!!

W załączeniu obrazek, z którego dumny powinien być każdy sprzedawca funduszy inwestycyjnych ? czerwonym kolorem nasza linia kapitału.

Ale zaraz, zaraz!?!?! Zarabiamy średnio tyle co rynek, ale jesteśmy lepsi? Tego nawet najbardziej wyrafinowany sprzedawca nam nie wmówi. Sprawdźmy może dokładniej. Może dane roczne, są zbyt „rzadko”. Sprawdźmy statystyki miesięczne. Średnia miesięczna zmiana indeksu WIG20 (od momentu jego publikacji) wynosi 1.32%. Jeśli miesięcznie zarabialibyśmy właśnie tyle, to na koniec 2006 roku powinniśmy mieć 7470 zł !!!

Ponad 2 razy więcej niż indeks WIG20. Do diabła?!?! Coś tu nie gra? Chyba nie to miał na myśli Einstein. A może to nie cud, tylko kuglarska sztuczka?

Gdzie leży odpowiedź? Proponuje zadawać to pytanie doradcom finansowym i różnego rodzaju zwolennikom długoterminowego inwestowania w akcje, na podstawie symulacji. Jeśli przejdą ten test poprawnie, być może warto z nimi dalej rozmawiać.

[Tekst z Archiwum GZ – oryginalny materiał, wraz z komentarzami]