Lorenz i polscy gimnazjaliści

„Bardzo drobna, umykająca naszej uwadze przyczyna może spowodować znaczny efekt, widoczny na końcu aż nadto. Mówimy wtedy, że jest on wywołany przez przypadek. Tymczasem to nie przypadek, to błąd, który popełniliśmy na początku naszych rozważań, tak potężnieje z czasem. Niedostrzeżone przez nas drobne różnice w warunkach początkowych mogą spowodować kolosalną różnicę w finale. Przewidywania staną się niemożliwe”. H. Poincare

W ostatnich dniach miały miejsce dwa z pozoru nie związane ze sobą wydarzenia. 16 kwietnia zmarł Edward Lorenz, zaś 23 kwietnia miał miejsce egzamin gimnazjalny z matematyki. Edward Lorenz znany jest jako jeden z pionierów Teorii Chaosu, zaś szczególnie sformułowania ?efekt motyla?. W dużym uproszczeniu chodzi o to, że w dużych o złożonych układach, nawet niewielkie i z pozoru nieznaczące działania, mogą mieć daleko idące konsekwencje. Lorenz w latach szcześdziesiątych zajmował się komputerowymi modelami, mającymi na celu prognozowanie pogody. Opracował układ kilkunastu równań, zawierających liczne parametry(np. tempretaura, siła i kierunek wiatru, ciśnienie) i zależności między nimi. Uznał, że wystarczą przybliżone dane wejściowe, aby otrzymać przybliżoną prognozę. W pewnym momencie okazało się, że prognozowane dane różnią się od siebie drastycznie, mimo pozornie tych samych danych wejściowych. Pozornie, gdyż okazało się, że w jednym z obliczeń Lorenz wykorzystał liczbę z dokładnością do trzech miejsc po przecinku, a innym razem do sześciu. Mimo tej pozornie nieznaczącej różnicy. Wyniki wyjściowe były drastycznie odmienne. Im dłuższy był czas prognozy tym różnice się zwiększały. Stąd wzięło się określenie ?efekt motyla? ? pozornie nieznaczące zdarzenie może mieć ogromny wpływ na cały układ ? motyl machający skrzydłami gdzieś na kuli ziemskiej, może być odpowiedzialny za huragan w zupełnie innym miejscu globu.
Co to ma wspólnego z egzaminem gimnazjalnym w Polsce i rynkiem finansowym? Teoria Chaosu zaczęła być wykorzystywana do opisywania zachowania rynków finansowych, które również są układem złożonym. Na tyle, że trudno dokonywać jakichkolwiek precyzjnych prognoz ? zbyt wiele potrzeba danych, zbyt wiele jest między nimi zależności, że maleńkie zdarzenie w jakiejś pozornie nieznaczącej gospodarce, może mieć wpływ na zachowanie się inwestorów w wielu częściach świata.

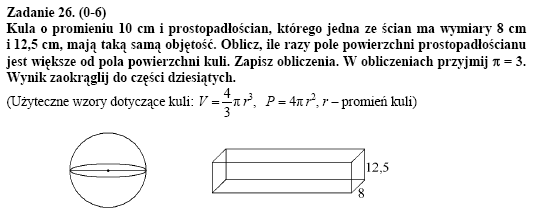
A egzamin? Oto treść jednego z pytań:

Bardzo mi się podoba podejście do uproszczeń. Krótko mówiąc, wiedza współczesnego gimnazjalisty jest gorsza, niż starożytnych Babilończyków, dla których pi wynosiło 3 1/8 oraz Egipcjan (3.1605), a od 1596 znamy ją z dokładnością do dwudziestu miejsc.
Właściwie czemu nie przyjąć dla uproszczenia, że to 5? Jest bardziej intuicyjne, niż 3. A, że od jakiegoś czasu słychać, że jest coraz mniej chętnych na studia politechniczne. No, cóż, zawsze możemy sprowadzać specjalistów z Chin, albo Indii. Bo inaczej, strach będzie choćby chodzić po mostach budowanych przez przyszłych inżynierów.