Patrząc na krzywą kapitału (equity) po raz pierwszy próbujemy ocenić jej atrakcyjność, posługując się typowo wzrokowymi kryteriami- gładkością i kątem nachylenia. Miss wszystkich takich krzywych pnie się w górę niemal pionowo i bez żadnych wypukłości.
To jak bardzo krzywa jest pofałdowana określa jej zmienność (czyli gwałtowność zmian), jedno z najważniejszych pojęć w inwestowaniu. Najprostszym jej miernikiem jest odchylenie standardowe (ang. standard deviation). To pojęcie znane ze statystyki służy do określenia zmienności samych cen instrumentów finansowych jak i wyników inwestycji (np. funduszu inwestycyjnego) i ma zawsze takie samo zadanie- określić jak szeroko wokół średniej rozrzucone są wszystkie badane wielkości. Zasada jest prosta: im większe skupienie wokół średniej tym mniejsza wartość odchylenia standardowego. Dla krzywej kapitału bez żadnych wypukłości, zbliżającej się kształtem niemal idealnie do linii prostej, wartość odchylenia standardowego dąży do zera.
Dla porządku wzór pomagający obliczyć odchylenie dla znanej, skończonej populacji jaką są na przykład historyczne wyniki dowolnego testu systemu transakcyjnego.
gdzie:
? (sigma) – to odchylenie standardowe
N – numer kolejnej obserwacji (tu- wynik każdej kolejnej transakcji)
Xi – wartość kolejnej obserwacji
X (z daszkiem) – średnia z wszystkich wartości obserwacji
W praktyce wzór nie wygląda aż tak odstraszająco. Najpierw sumujemy wartości wszystkich kolejnych obserwowanych wartości i wyciągamy z nich zwykłą średnią arytmetyczną. Następnie od każdej kolejnej wartości obserwacji odejmujemy ową uzyskaną średnią i podnosimy wynik do kwadratu. Sumujemy wszystkie tak uzyskane kwadraty i wyciągamy z nich pierwiastek. Odchylenie ma taką samą miarę jak poszczególne obserwacje czyli jeśli liczymy odchylenie od średniej dla kolejnych cen akcji notowanych w PLN to będzie ono również miarą rozproszenia podaną w PLN.
W zasadzie raporty systemów nie podają odchylenia standardowego ale wchodzi ono w skład innego ważnego miernika- wskaźnika Sharpa. Odchylenia standardowego używa się natomiast we Wstęgach Bollingera, można je również używać zamiennie z ATR w strategiach (choćby w tej wybicia ze zmienności). Odchylenie podają też czasami fundusze w swoich wynikach. Fundusze obligacji powinno charakteryzować dużo niższe odchylenie niż akcyjne.
Zakłada się ze względów praktycznych, że wartości obserwacji mają rozkład normalny, co w finansach nie jest niestety prawdą gdyż istnieją zdarzenia, które wychylają się dość znacznie od średniej. Taleb nazywa je właśnie Czarnymi Łabędziami (Black Swans) gdyż ich istnienie choć niesamowicie rzadkie jest jednak możliwe. Inną ich popularnie spotykaną nazwą jest ?six sigma” co wzięło się właśnie z odchyleń standardowych. Statystycznie jest tak, że w obrębie jednego odchylenia (1 sigma) poniżej i powyżej średniej znajduje się 68% obserwowanych wartości (np. 68% cen zamknięcia danej akcji). Drabinka wygląda tak:
68% wartości leży w odległości 1odchylenia (1 sigma) od średniej;
95,5% wartości leży w odległości 2 odchyleń (2 sigma) od średniej;
99,7% wartości leży w odległości 3 odchyleń (3 sigma) od średniej;
Dochodząc do 6 sigma (six sigma) otrzymujemy zdarzenie, które leży w obszarze nieprawdopodobnie odległym od średniej wartości (oczekiwanej).
Należałoby też podkreślić, że małe odchylenie standardowe (gładka w miarę krzywa) czyli mała zmienność nie oznacza małego ryzyka ! Słynne ostatnio na świecie amerykańskie obligacje hipoteczne o podwyższonym ryzyku miały niskie odchylenie a mimo to jednorazowe ryzyko okazało się dla nich zabójcze!
I mały, podchwytliwy teścik na koniec:
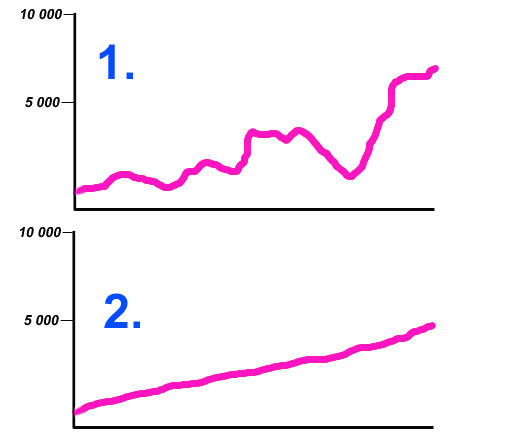
Poniższe krzywe kapitału 2 systemów zostały wygenerowane z tej samej wartości początkowej. (1) ma spore odchylenie, w (2) zbliża się ono do zera. Którą krzywą chcielibyście widzieć w swoim systemie?
Najczęstsza odpowiedź to equity nr. 2. Ja podpowiem, że to dobra i zła odpowiedź jednocześnie. Dlaczego ? To już w kolejnym wpisie o ile ktoś wcześniej nie błyśnie całkiem rzeczową podpowiedzią 🙂
–* Kathay *–

24 Komentarzy
Dodaj komentarz
Niezależnie, DM BOŚ S.A. zwraca uwagę, że inwestowanie w instrumenty finansowe wiąże się z ryzykiem utraty części lub całości zainwestowanych środków. Podjęcie decyzji inwestycyjnej powinno nastąpić po pełnym zrozumieniu potencjalnych ryzyk i korzyści związanych z danym instrumentem finansowym oraz rodzajem transakcji. Indywidualna stopa zwrotu klienta nie jest tożsama z wynikiem inwestycyjnym danego instrumentu finansowego i jest uzależniona od dnia nabycia i sprzedaży konkretnego instrumentu finansowego oraz od poziomu pobranych opłat i poniesionych kosztów. Opodatkowanie dochodów z inwestycji zależy od indywidualnej sytuacji każdego klienta i może ulec zmianie w przyszłości. W przypadku gdy materiał zawiera wyniki osiągnięte w przeszłości, to nie należy ich traktować jako pewnego wskaźnika na przyszłość. W przypadku gdy materiał zawiera wzmiankę lub odniesienie do symulacji wyników osiągniętych w przeszłości, to nie należy ich traktować jako pewnego wskaźnika przyszłych wyników. Więcej informacji o instrumentach finansowych i ryzyku z nimi związanym znajduje się w serwisie bossa.pl w części MIFID: Materiały informacyjne MiFID -> Ogólny opis istoty instrumentów finansowych oraz ryzyka związanego z inwestowaniem w instrumenty finansowe.

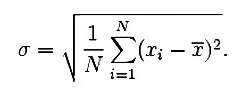
equity nr. 2 może być wynikiem nadmiernej optymalizacji systemu.
(?)
zimno… obie equity są bez optymalizacji
W systemie 2 mozna uzyc wiekszej dzwigni, wtedy wynik wzrosnie wykladniczo.
to pewnie w tej equity nr 1 była użyta –
——-
equity nr 2 – stała liczba kontraktów
equity nr 1 – zmienna
(?)
osobiście wolę linię nr.2 : może tu być inne zarządzanie ,inna dywersyfikacja ,przy dużym lewarze mogą być nierealistyczne oczekiwania co do przyszłości i może go dosięgnąć black swans ,szczególnie jak zacznie ten system nr.2 stosować większa liczba graczy (stanie się ogólno dostępny).
No i jeden może obejmować 15 lat a drugi 2 lata i nie widać reszty…
W każdym systemie w nieograniczonym czasie rynek testuje wszystkie dostępne kombinacje – 10-sigma też 😉
No i wreszcie 1 jest trudna (psychicznie) w stosowaniu -wielu graczy poddaje się na przesileniach ,a 2 linia łatwa.
Podejrzewam, że stosując do 1 technikę wybicia z kanału można wyciągnąć dużo więcej niż z 2. Ale ryzyko i tak pozostanie większe.
Nr 1 wieksza zmiennosc, wiecej transakcji , rozpalona glowa….
Pytanie trochę przewrotne. Człowiek "kupuje oczami".
Wybór strategi wydaje mi się zależna od tego, jaką wartosć przyjmie inwestor za kluczową. Jeżeli MaxProfit, to wykres 1-szy, jeżeli MinDD wtedy2-gi.
Na pierwszym jednak kreśląc linie odchyleń standardowych, łatwiej wychwycić wrażliwość systemu.
Rzeczowa podpowiedź jest już chyba w tekście …
zależność od dywersyfikacji i rodzaju instrumentów przy czym wykres nr 1 nie moze dać ponad przeciętnego zysku mimo ze to średnia WŁASNEGO tempa
ilość transakji przy wykresie 2 może być niższa niż przy wykresie 1
wykres nr 2 tak naprawdę to wykres części agresywnej portfela nr 1 tyle ze jest ignorowany pewnie dlatego ze stanowi małą część porfela
wykres nr 1 oparty na obligacjach wykres nr 2 bardziej agresywny
nie ma możliwości inwestując agresywnie wyrysować wykres nr 1
wykres nr 1 to zysk klienta brutto
wykres nr 2 to zysk BM na tym kliencie
😉
oczywiście z wiadomych względów to nie jest rozwiązanie testu
"Sam w sobie" lepszy wydaje się system (2.), bo mniej ryzykowny, a zyskowność podobna. Ale system (1.) można wykorzystać jako część większej strategii. Mimo wszystko daje większy zysk niż (2.), a po dodaniu jakiegoś (jakichś) nieskorelowanego dodatnio walorów można krzywą wygładzić nie tracąc na atrakcyjniejszej stopie zwrotu. To tak w skrócie i na chłopski rozum 😉
@Jacek!
Też tak myślę:-)
Pozdrowienia,
GiełduGiełdu
Jacek trafiłeś w 10 !!!
😉
..
ciekawe, co na to KatHay ?
no to kathay zrobił nam "kaizen" :))
ciekawe do czego dazy ?
do przejscia do innej miary ryzyka niż zmienność ?
pokazania wad związanych z liczeniem SD ?
oczywistą oczywistościa jest wybranie wizualnie krzywej zblizonej do 2 tylko tutaj mamy do czynienia na pewno z niższa spodziewana stopa zwrotu niż przy krzywej o wyższym sd…
jedyna odpowiedź w tym przypadku która jest dobra i zła dla mnie wynika wlaśnie z liczenia odchylenia standardowego od średnej które jest liczone zarówno w naszą niekorzystna stronę jak i niestety w korzystną czyli w plus tez za daleko nie odskoczymy…
pozostaje czekac na odpowiedź
ps. a propo six sigma od razu przychodzi mi na myśl Toyota {lean six sigma} vs Renault czyli spodziewana brzydka acz niezawodna Toyota i nieoczekiwana acz kosztowna, ekstrawagancka i awaryjna Megane. Jak kto lubi :))
Coś mi mówi, że w dobrym kierunku poszedł @marek poruszając wątek czasu. Tylko, że moim zdaniem wykresy mogą przedstawiać skale nie np. 15- i 2-letnie, ale np. … kilkudniowe. A liczba obserwacji ("i" z podanego wzoru) jest zbyt mała, żeby wyciągać sensowne wnioski. Co prawda stopa zwrotu wynosząca kilkaset % jest mało prawdopodobna do osiągnięcia w tak krótkim okresie, ale przy dużej dźwigni możliwa. Dalsza część wykresu nie musi być powtórzeniem wykresów podanych w przykładzie. Teoretycznie możliwa jest sytuacja, że w czasie dwa razy dłuższym system (1.) powtórzy swój wynik, a (2.) sprowadzi kapitał do punktu wyjścia.
Jeszcze inna możliwość: na wykresie (2.) krzywa kapitału jest praktycznie linią prostą. Jeśli skala cenowa jest arytmetyczna (trudno to jednoznacznie stwierdzić na postawie dwóch liczb;-)), to by oznaczało, że procentowa stopa zwrotu w miarę upływu czasu maleje i nie da się powtórzyć osiągniętego wyniku w przyszłości 😉
ciekawe to wszystko, ciekawe 🙂
nie podałem wiecej szczegółów zupełnie świadomie żeby sprawdzić reakcję na samą surową equity…
postaram się w weekend zrobić to podsumowanie choć przy takich meczach trudno oderwać się od TV 🙂
Moim zdaniem, sprawa jest prosta.
Krzywa 1 podaje wyniki dla systemu o małej liczbie transakcji, a krzywa 2 dla systemu o dużej liczbie transakcji.
W tym 2 przypadku stosujemy bliższe stopy, więc w efekcie otrzymujemy krzywą o mniejszych odchyleniach.
Wada krzywej 2 to natomiast… kasa odprowadzana do BM, która jest przecież wprost proporcjonalna do liczby transakcji.
Pozdrowienia,
GiełduGiełdu
A ja myślę, że Kathay robi nam test Rorschacha w wersji dla spekulantów 🙂
na pewno dobrze się bawi przy lekturze postów 🙂
>To jak bardzo krzywa jest pofałdowana określa jej zmienność (czyli gwałtowność zmian), jedno z najważniejszych pojęć w inwestowaniu.
>Dla krzywej kapitału bez żadnych wypukłości, zbliżającej się kształtem niemal idealnie do linii prostej, wartość odchylenia standardowego dąży do zera.
Kathay, najwyrazniej przyjales kilka ukrytych zalozen. Odchylenie stand. nie nadaje sie do mierzenia zmiennosci krzywej na podstawie wartosci, ktore ta krzywa laczy. W trendzie rosnacym albo malejacym wartosc odchylenia bedzie ogromna i bedzie slabiutko przydatna.
Twoje drugie zacytowane przeze mnie zdanie jest wiec bledne. Do zera bedzie dazyc wartosc st.dev., jesli krzywa kapitalu bedzie plaska (nachylenie 0 stopni), a nie bez wypuklosci.
Stosowanie odchylenia ma sens, jesli mierzona wartoscia sa np. procentowe wachniecia kapitalu. Wtedy uzyskamy odchylenie zmiennosci kapitalu.
Zakładam oczywiście, że obserwacje we wzorze to kolejne zmiany kapitału w transakcjach. Im wyższe (aż po fat tails) w obie strony tym większe rozproszenie.
Dzięki za tą uwagę! Dodam bo rzeczywiście czytając pod tym kątem nie wydaje się to tak oczywiste !